Hough Transform
Hough Transform은 voting을 통해 이미지 내의 점에 선을 fitting하는 기법이다.
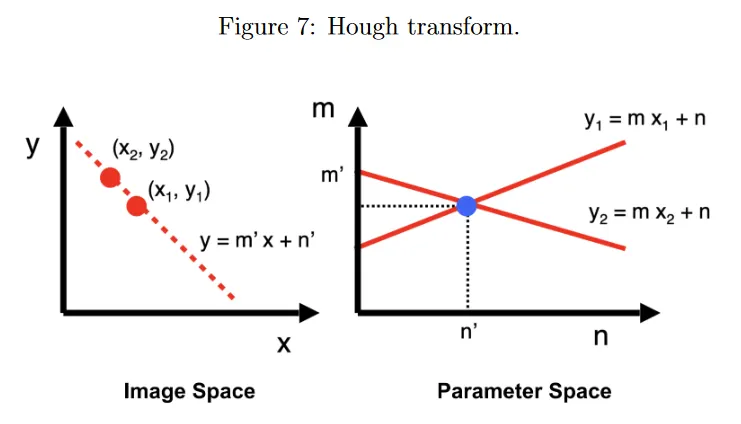
아래 그림 왼쪽과 같이 이미지 공간에서 점의 시리즈 에 형식의 선을 fit하기를 원한다고 하자. 이 선을 찾기 위해 아래 그림 오른쪽에 나온 dual parameter 또는 Hough space를 고려한다. 선 상에 존재하는 이미지 공간의 점 은 파라미터 공간에서 선 이 된다. 역으로 파라미터 공간에서 점 은 이미지 공간에서 으로 주어지는 선이 된다.
파라미터 공간의 선 는 이미지 공간의 점 를 통과하는 이미지 공간의 모든 선을 나타낸다. 따라서 이미지 공간의 점 과 를 모두 지나는 선을 찾으려면 두 점을 Hough space의 선과 연관시켜서 교차점 을 찾으면 된다. 이 Hough space의 점은 이미지 공간의 두 점을 모두 지나는 선을 나타낸다.
실제로는 파라미터 공간에 대해 width 인 정사각형 셀로 이루어진 이산 grid로 Hough space를 나눈다. 초기에 모든 에 대해 을 중심으로 하는 셀의 갯수 격자 을 유지한다. 이미지 공간의 모든 데이터 포인트 에 대해 를 만족하는 모든 을 찾아 갯수를 1 증가시킨다. 모든 데이터 포인트에 대해 이 작업을 수행하면 Hough space에서 가장 높은 갯수를 가진 점 이 이미지 공간의 fit 된 선을 나타낸다. 이제 왜 이것이 voting 절차인지 알 수 있다. 각 데이터 요소 는 이미지 공간 각 후보 line 에 대해 최대 1표를 투표할 수 있다.
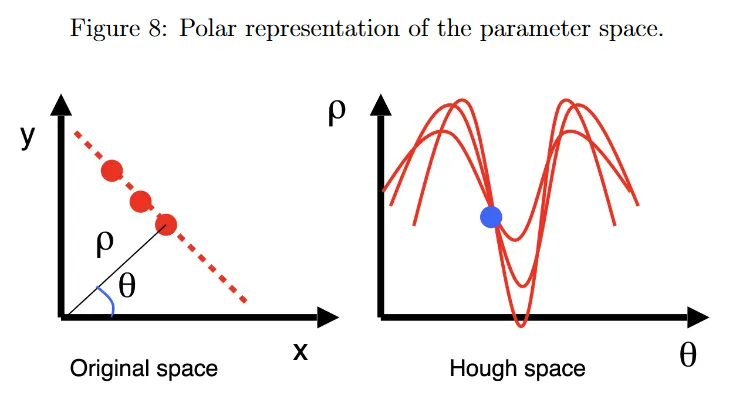
그러나 이미지 공간에서 선의 기울기는 로 unbounded이다. 이로 인해 Hough voting이 계산과 메모리 집약 알고리즘이 된다. 이를 해결하기 위해 아래 그림과 같이 polar 파라미터화를 사용한다.
위 그림 왼쪽에서 는 원점에서 선까지의 최소 거리(이미지 크기 또는 데이터셋에서 임의의 두 점 사이의 최대 거리로 bound 됨)이고, 는 x축과 선의 normal vector 사이의 각도(0과 사이로 bound 됨)이다. 이전과 동일한 Hough voting 절차를 사용하지만 Cartesian space에서 특정한 를 지나는 모든 가능한 선은 이제 통해 Hough space에서 sinusoidal profile에 해당한다. 위 그림 오른쪽 참조.
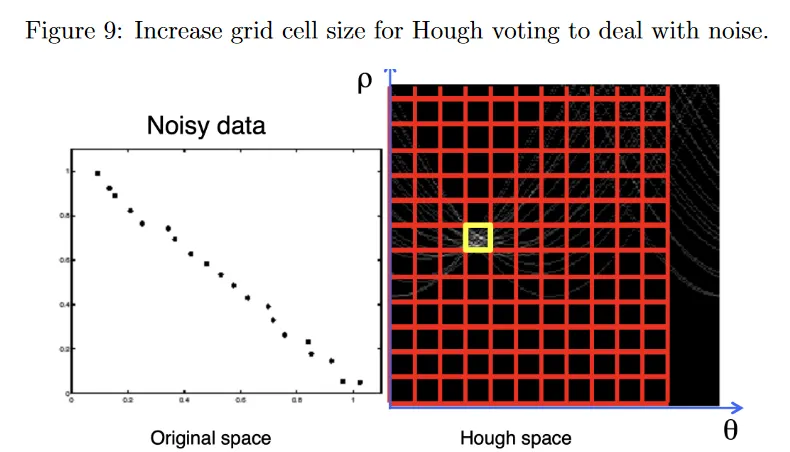
실제로 noisy 데이터 점은 이미지 공간에서 동일한 선 상의 점들에 해당하는 Hough space의 sinusoidal profile이 Hough space에서 반드시 동일한 점에서 교차하지 않을 수 있다. 이것을 해결하기 위해 아래 그림에 나온 것처럼 grid cell의 width 를 증가시켜서 불완전한 교차점에 대한 허용 오차를 증가시킬 수 있다.
이렇게 하면 noisy 데이터를 다루는데 도움이 되지만 조정해야 하는 또 다른 파라미터가 생긴다. 작은 grid 크기는 noise 때문에 이미지 공간의 선을 놓칠 수 있는 반면, 큰 grid 크기는 모든 내의 셀이 가능한 선이기 때문에 다른 선을 병합하고 추정 정확도를 낮출 수 있다.
또한 이미지 공간에 uniform noise가 존재하면, Hough space에 spurious(허위) peak가 존재할 수 있고 적절한 모델에 대한 명확한 consensus가 없게 된다.