Search
Duplicate

수학/ Half-normal, Sub Gaussian, Super Gaussian 분포

Half-normal

•
어떤 문제에서 음이 아닌(non-negative) 실수에 대한 분포를 원할 수 있다. 한 가지 방법은 Y=∣X∣Y = |X|를 (X∼N(0,σ2)X \sim \mathcal{N}(0,\sigma^2)) 정의하는 분포를 만드는 것이다. YY에 대해 유도된 분포는 half-normal 분포라고 부른다. pdf는 다음과 같다.
N+(y∣σ)≜2N(y∣0,σ2)=2σpiexp⁡(−y22σ2) y≥0\mathcal{N}_+(y|\sigma) \triangleq 2\mathcal{N}(y|0,\sigma^2) = {\sqrt{2} \over \sigma\sqrt{pi}} \exp\left( - {y^2 \over 2\sigma^2} \right) \ y \ge 0
•
이것은 N(0,σ2)\mathcal{N}(0,\sigma^2) 분포를 접은 것으로 생각할 수 있다.

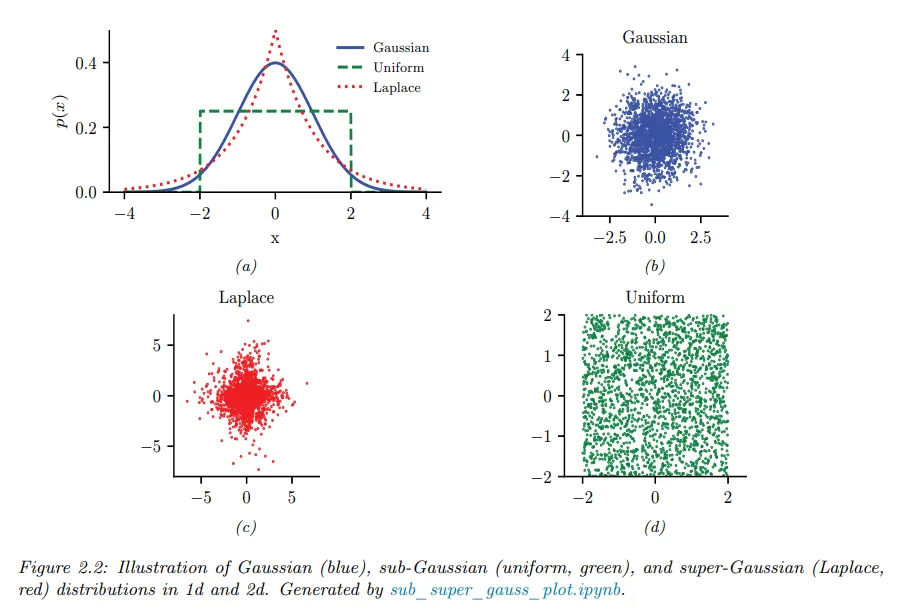
Sub-Gaussian and Super-Gaussian distributions

•
가우시안 분포의 2가지 주요 변종이 있다.
◦
super-Gaussian 또는 leptokurtic(’Lepto’는 그리스어로 ‘얇은’이라는 뜻이다)과 sub-Gaussian 또는 platykurtic(’Platy’은 그리스어로 ‘넓은’ 이라는 뜻이다)이 그것이다.
◦
이 분포들은 꼬리가 얼마나 두꺼우냐 얇으냐를 측정하는 kurtosis(첨도)의 측면에서 차이가 있다(즉 밀도가 평균에서 0으로 사라지는 속도). 더 정확하게 kurtosis는 다음과 같이 정의된다.
kurt(z)≜μ4σ4=E[(Z−μ)4](E[(Z−μ)2])2\text{kurt}(z) \triangleq {\mu_4 \over \sigma^4} = {\mathbb{E}[(Z-\mu)^4] \over (\mathbb{E}[(Z-\mu)^2])^2}
•
여기서 σ\sigma는 표준편차이고 μ4\mu_4는 4차 중심 적률(central moment)이다.
◦
따라서 μ1=μ\mu_1 = \mu는 평균이고, μ2=σ2\mu_2 = \sigma^2은 분산이다.
◦
표준 가우시안에서 첨도는 33이다. 따라서 어떤 사람들은 초과(excess) 첨도를 첨도에서 3을 뺀 값으로 정의한다.
•
라플라스 분포 같은 super-gaussian 분포는 양의 초과 첨도를 갖고 따라서 가우시안 보다 두꺼운 꼬리를 갖는다.
◦
균등 분포 같은 sub-gaussian 분포는 음의 초과 첨도를 갖고 따라서 가우시안 보다 얇은 꼬리를 갖는다.
◦
아래 그림 참조

참조

Made with