Weak Perspective Model
Weak Perspective Model은 3d 객체를 2d 평면에 투영하는 간소화된 모델로 일반적인 Perspective Projection 모델에 비해 계산이 덜 복잡하다는 장점이 있다. 계산이 단순하기 때문에 부정확하지만, 객체가 작고 카메라에서 먼 경우(깊이의 변화가 작거나 작은 시야각)에 좋은 근사치를 구할 수 있다.
weak perspective model은 2단계로 3d 점을 2d로 투영하는데, 우선 orthogonal projection을 사용하여 카메라와 객체 사이에 존재하는 가상의 reference plane에 투영한 다음, projective transformation을 사용하여 image plane에 투영한다.
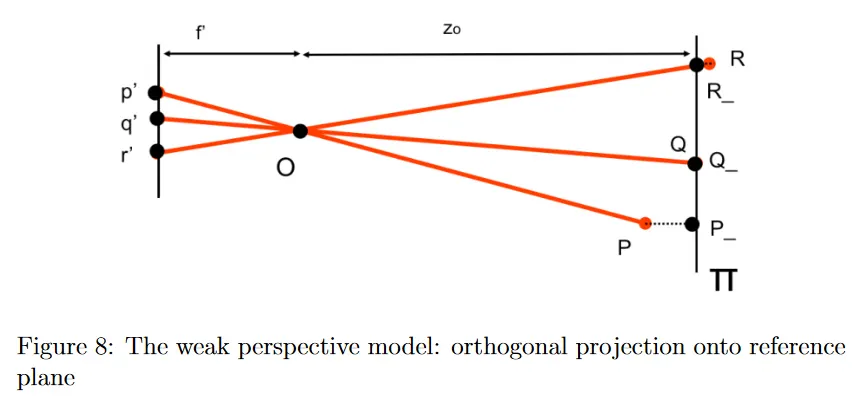
우선 아래 그림과 같이 카메라 중심에서 거리 (객체의 평균 깊이) 만큼 떨어진 가상의 reference plane 가 주어질 때, 3d 점 을 우선 orthogonal projection을 사용하여 (해당 3d점의 깊이를 로 치환) 평면 에 투영한 다음 점 을 생성한다. (아래 이미지는 왼쪽이 카메라의 image plane이고 오른쪽이 real world에서 객체의 평균 깊이에 해당하는 reference plane이다)
이것은 카메라에서의 depth deviation가 평면까지의 거리에 비해 작을 때 합리적인 근사이다.
reference plane에 투영된 객체의 좌표는 다음과 같이 정의된다. 객체의 depth를 평균 깊이 로 대체한다.
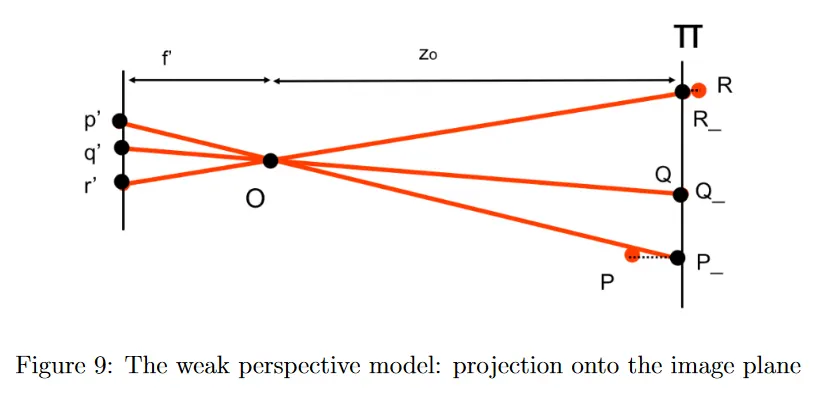
그 다음으로 reference plane에 투영된 3d 점들에 대해 일반적인 projective transformation을 수행하여 이미지 평면에 투영하고 점 을 생성한다.
결국 이미지 평면에 투영된 점은 다음과 같이 정의된다.
각 점의 depth를 로 근사했기 때문에 투영은 단순한 상수 배율로 축소된다. 이 배율은 focal length를 로 나눈 것과 동등하다.
이 모델은 projection 행렬로 단순화 된다.
이미지 평면 상의 점은 결국 depth와 관계 없이 원래 3d 점의 배율이 되며, 따라서 projective transform의 비선형성은 사라지고 weak perspecrtive transformation은 단순한 확대기가 된다.
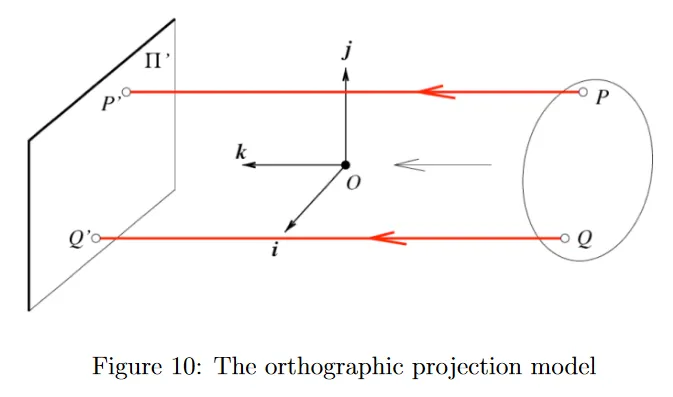
Orthographic Projection Model
weak perspective model에서 더 나아가서 orthographic(or affine) projection model로 단순화 할 수 있다. 이 경우 optical 중심이 무한대에 존재하고 projection ray는 retinal plane에 수직이 된다. 그 결과 모든 depth를 무시하고 다음과 같이 된다.
Orthographic projection 모델은 종종 건축과 산업 디자인에서 사용된다.