•
이전에 들었던 유사한 부분이 많기 때문에 간략히 정리. 상세 내용은 아래 페이지 참조
•
train data의 noise까지 fitting 된 것을 overfitting이라고 한다.
•
모델이 학습이 안된거는 underfitting
•
과적합 문제를 방지하기 위해 Regularization(규제)을 사용함. 이것은 overfitting을 방지한다.
◦
Regularization은 일종의 페널티를 부여한다.
◦
예컨대 회귀 문제는 를 최소화하는 것을 찾게 되는데, 여기에 의 합을 더해줘서 (절대값을 더할 수도 있고(이게 L1) 제곱해서 더할 수도 있다(이게 L2)) (추가로 를 곱한) 무작정 를 최소화하는 것을 못 찾게 한다.
◦
머신러닝에서는 가중치 를 구하게 되는데, 이 를 강제로 더해줘서 규제를 사용함
•
기본적으로 복잡한 선을 그리려면 함수가 복잡해져야 한다.
◦
위 overfitting 이미지에서 가장 오른쪽의 복잡한 선을 그리려면 그 식 안에 속한 의 값이 커야 함. 만일 가 0에 가까운 작은 값이라면 복잡한 선을 그릴 수 없고, underfitting과 같은 단순한 선이 그려짐.
◦
그래서 단순한 모델을 만드는 것과 weight 값을 작게 만드는 것은 강한 상관관계가 있다.
◦
이래서 머신러닝에서 학습을 반복하면 가 점점 커지게 되는데, (식은 최소화된 를 잡게 되므로 그 안에서 작은 값을 찾게 되지만) 이거를 방지하기 위해 아예 를 더해줘서 균형을 잡는다.
•
L2 Regularization을 Ridge Regression이라고 한다.
◦
제곱의 합이기 때문에 원형으로 나타나고, 가 커질수록 원은 작아지고 작아질수록 원은 커짐.
•
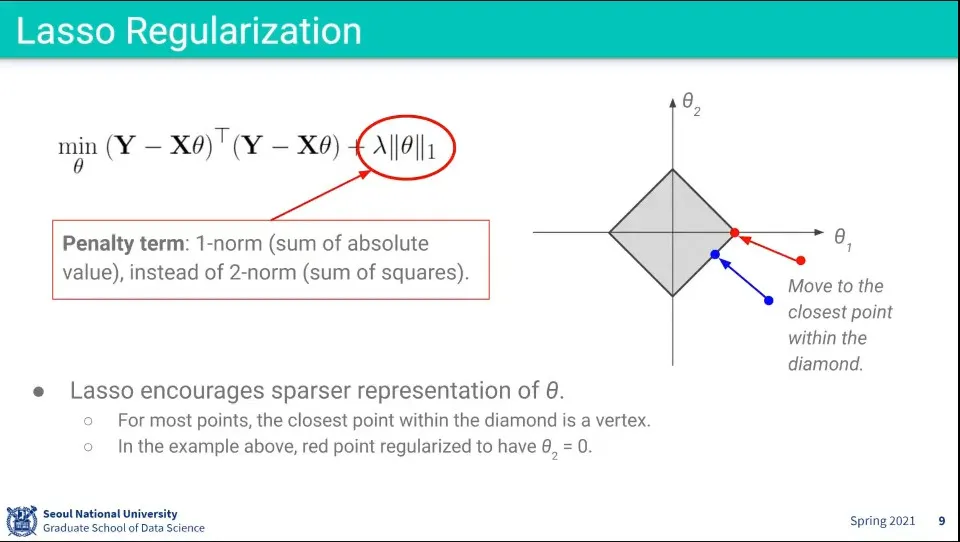
L1 Regularization을 Lasso Regularization이라고 한다.
◦
아까와 마찬가지로 가 커질수록 마름모는 작아지고 작아질수록 커짐.
◦
L2와 달리 절대값의 합이기 때문에 마름모 모양으로 표현된다.
◦
이 경우 많은 경우 최적값이 꼭지점에 모이게 되는데, 마름모 바깥의 많은 점들의 가장 가까운 거리가 꼭지점에 대응되기 때문. 변에 대응되는 영역은 좁은 영역만 가능하다.
◦
많은 점들이 꼭지점에 모인다는 것은 가 0이 된다는 것이 되고, 그것은 위의 복잡한 수식에서 많은 선들이 사라져서 결국 식이 단순해 진다는 것이 된다.
◦
따라서 noise에 robust한 decision boundary를 만들게 된다.
•
Neural Network는 overfitting이 쉽게 되기 때문에 위와 같은 기법을 사용ㅎㅏ.
•
선형회귀에서 Regularization을 했던게 Weight Decay이다.
◦
L1, L2 처럼 절대값을 더하거나 제곱을 더하거나 할 수 있음
•
Multi layer에도 마찬가지로 적용 가능
•
Early Stopping은 Overfitting이 발생하기 전에 멈추는 것
•
멈추는 시점은 어떤 기준을 가지냐에 따라 달라질 수 있음
•
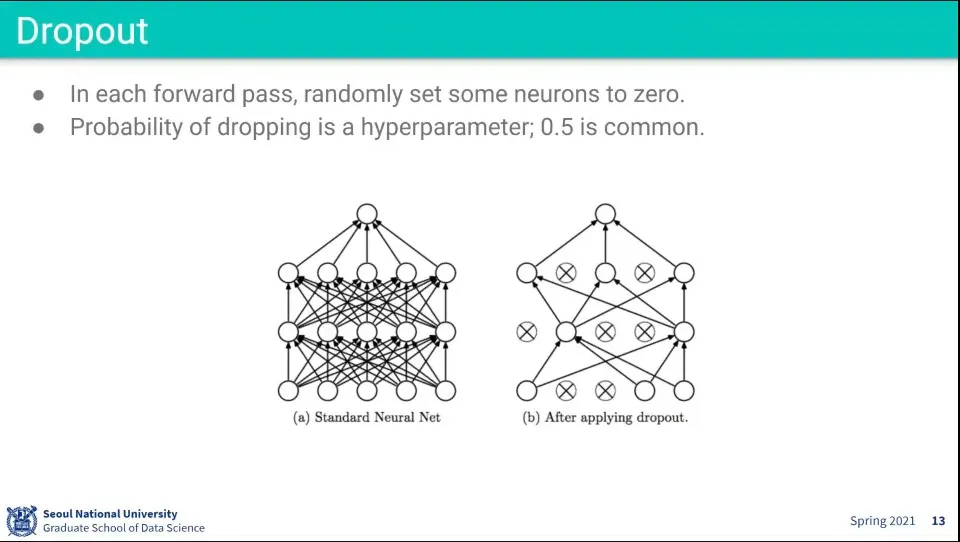
Forward pass에서 일부 노드를 랜덤하게 제거한 후에 학습을 수행하는 것이 Dropout
•
만일 이미지에서 어떤 두드러진 feature가 있다면 컴퓨터가 해당 feature에만 최적화될 수 있음. 그러면 일반화가 안 되기 때문에, 일부러 해당 feature를 가리고 학습시켜서 다른 feature들을 보고도 인식할 수 있게 함.
•
dropout은 학습할 때만 적용하고 테스트할 때는 사용하지 않는다.
•
dropout을 구현한 코드 예시
◦
일부 node를 끄면 학습 scale이 달라지기 때문에 그 scale을 맞추기 위해 가려지는 확률만큼 스케일을 키워서 학습해야 한다.
•
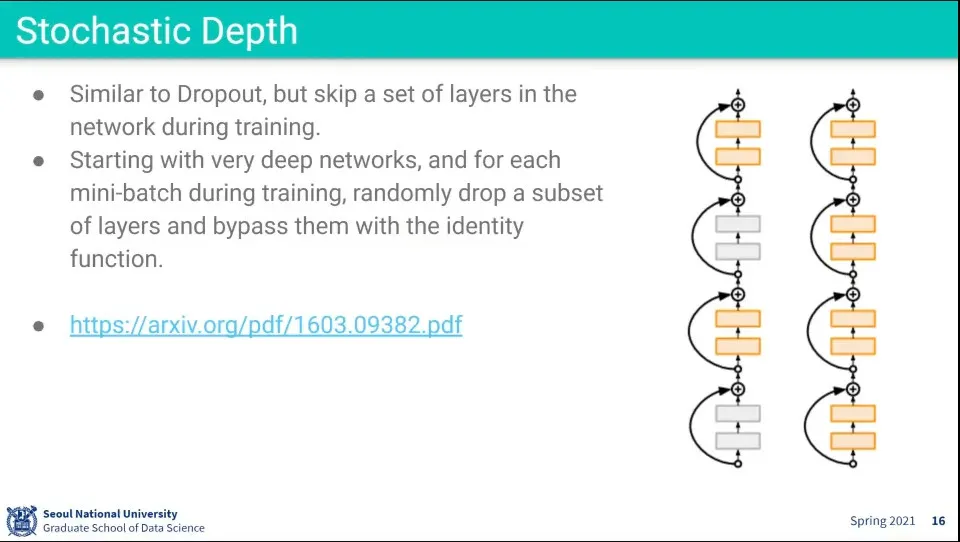
Stochastic Depth는 dropout이랑 비슷함
◦
랜덤하게 layer를 건너 띄고 학습하는 것
•
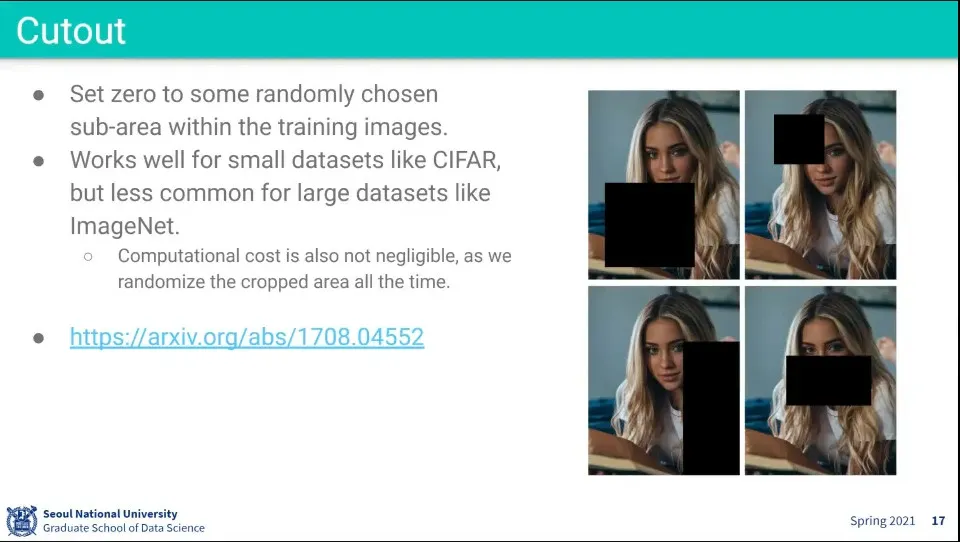
데이터의 자체를 아예 가려서 학습
◦
데이터가 작을 때는 많이 썼는데, 데이터가 클 때는 실용적이지는 않다.
•
dropout은 써라
•
batch normalization도 써라
•
data augmentaion도 해라
•
early stopping도 적절히 활용해라
•
Stochastic Gradient Descent도 몇 가지 문제가 있음
◦
한쪽 Gradient가 급격히 변할 때 원하는 방향으로 빠르게 못 가고 지그재그 함
◦
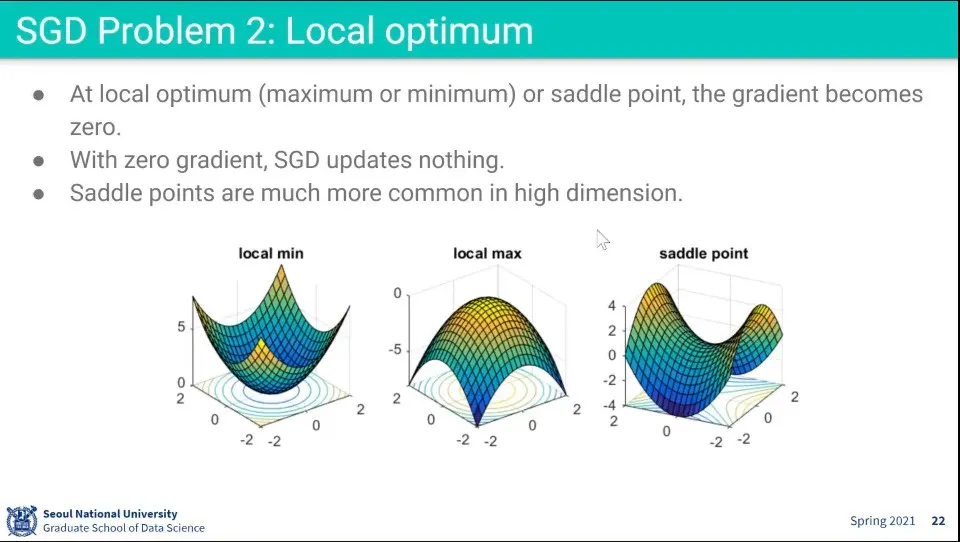
Saddle point를 만나면 미분이 0이 나와서 멈춤
◦
데이터가 아주 크면 mini-batch가 데이터 전체에 대해 대표하기 어려움
•
경사에 깊은 방향으로 크게 움직여서 지그재그를 만듦
•
dimension이 높아질수록 saddle point가 빈번하게 발생함
•
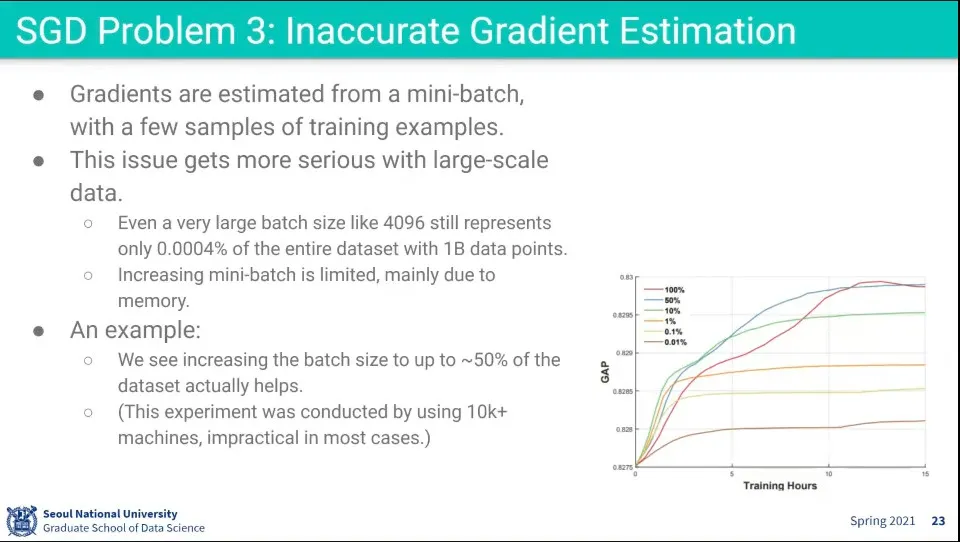
데이터가 아주 크면 batch가 전체를 대표한다고 보기 어려움
◦
batch는 물리적인 메모리 크기 한계로 일정 이상 커지기 어려움
◦
batch가 커지면 성능이 좋아짐 —50%까지는 늘어날수록 성능이 좋아짐. 물론 그 이상 올라가면 성능이 크게 좋아지지 않음
•
물리학에서 Momentum과는 개념이 좀 다르지만 여튼 SGD에 Momentum을 이용해서 SGD를 개선할 수 있음
◦
물리학에서 inertia(관성)는 어떤 물체가 운동을 유지하려는 성질의 정도이고 momentum은 어떤 물체가 얼마나 빠르게 운동하는지를 정량적으로 나타내는 정도. momentum은 mass와 velocity의 곱으로 표현 됨.
◦
여기서 말하는 말하는 Momemtum은 사실 관성(inertia)에 가까움
•
전 단계의 velocity에 상수()를 곱해서 현재 gradient에 더해 줌
◦
이 과정이 일종의 history처럼 작용해서 한 방향으로 이동하고 있었으면 그 방향으로 힘을 더 해줌
◦
이러면 지그재그를 덜하고 더 빠르게 움직일 수 있음
◦
이렇게 하면 saddle point를 통과할 수 있음. 미분은 0이지만 관성이 있었기 때문에 움직일 수 있음
•
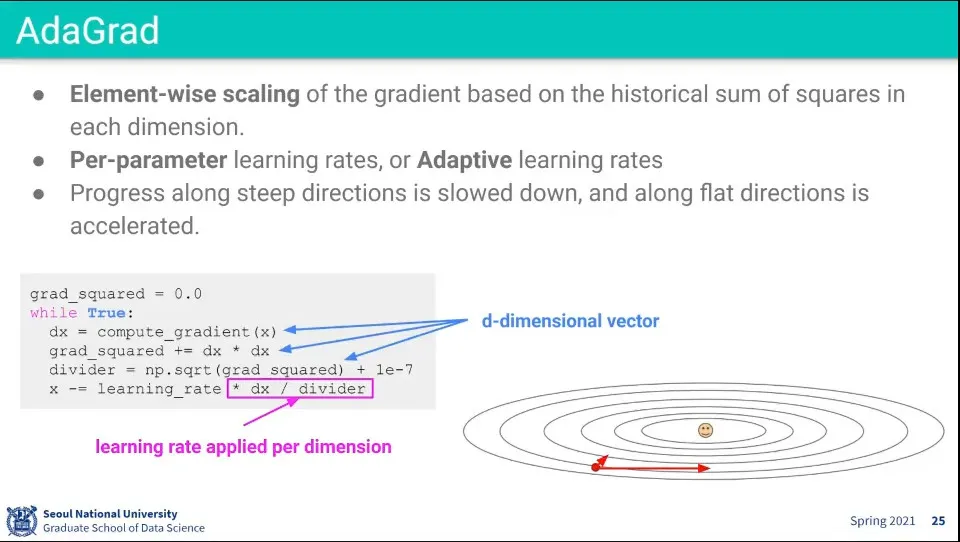
Element-wise로 scaling을 해준다.
◦
Gradient의 제곱해서 grad_squared 값을 구하고 그것을 dx를 나눈 값을 사용함
◦
grad_squared을 누적한다는게 중요한데, 이렇게 하면 나눠주는 값이 점점 커짐.
◦
따라서 gradient가 컸던 곳에서는 값을 나눠주므로 작아지게 하고, gradient가 작았던 곳에서는 값을 키워줘서 적절한 방향으로 움직일 수 있게 해줌
◦
축마다 다르게 계산되어서 경사가 급했던 곳은 빠르게, 완만했던 곳은 천천히 가게 해준다.
•
그런데 AdaGrad는 과거를 양수(제곱했으므로)로 누적하기 때문에 분모가 커지기만 함.
◦
이래서 시간이 지날수록 분모가 커져서 업데이트가 점점 느려짐
◦
이것을 보완하기 위해 과거 데이터를 decay 시켜 주는게 Leaky AdaGrad. RMSprop이라고도 한다.
•
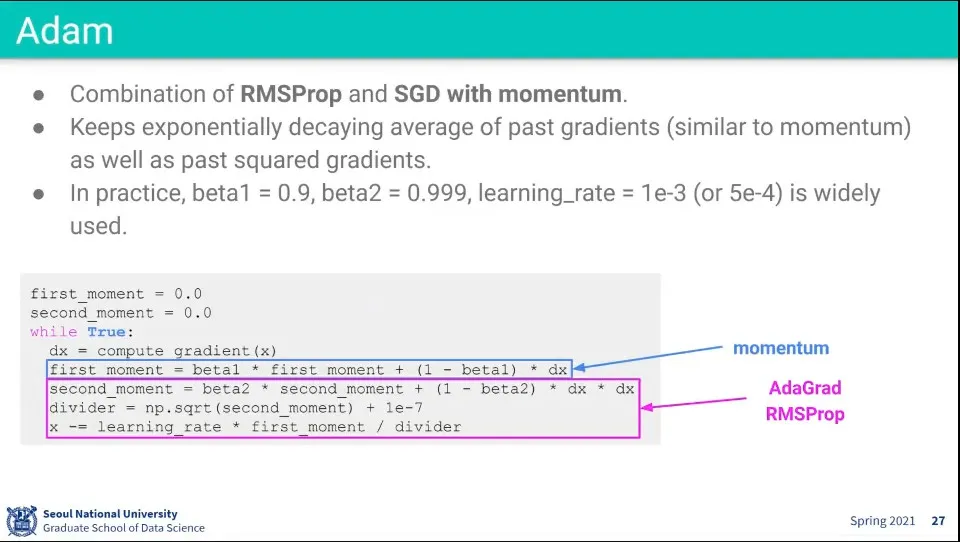
Adam은 RMSProp과 AdaGrad를 합한 것
◦
가장 발전된 방법이기 때문에 일단 시작할 때는 Adam으로 시작함
•
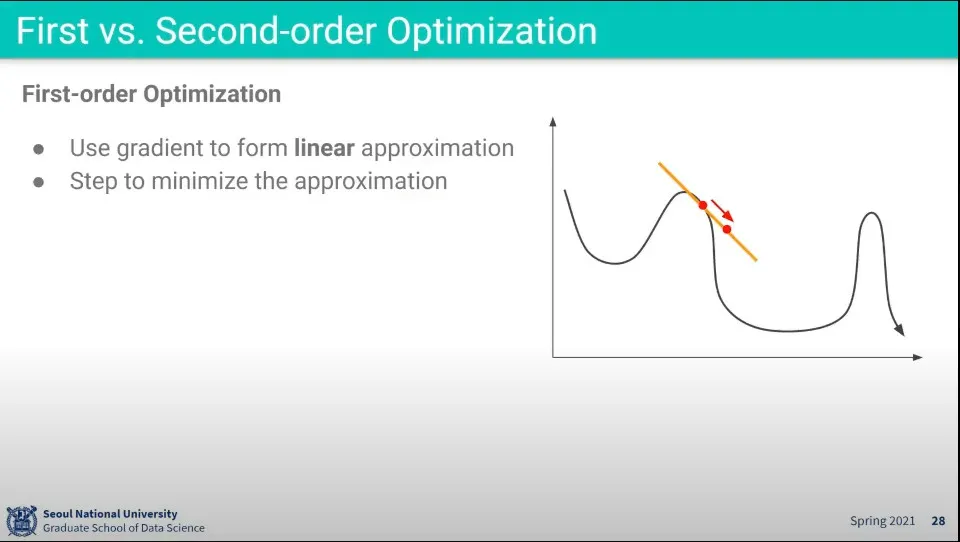
지금까지 한 것은 1차식으로 최적화 했던 것
•
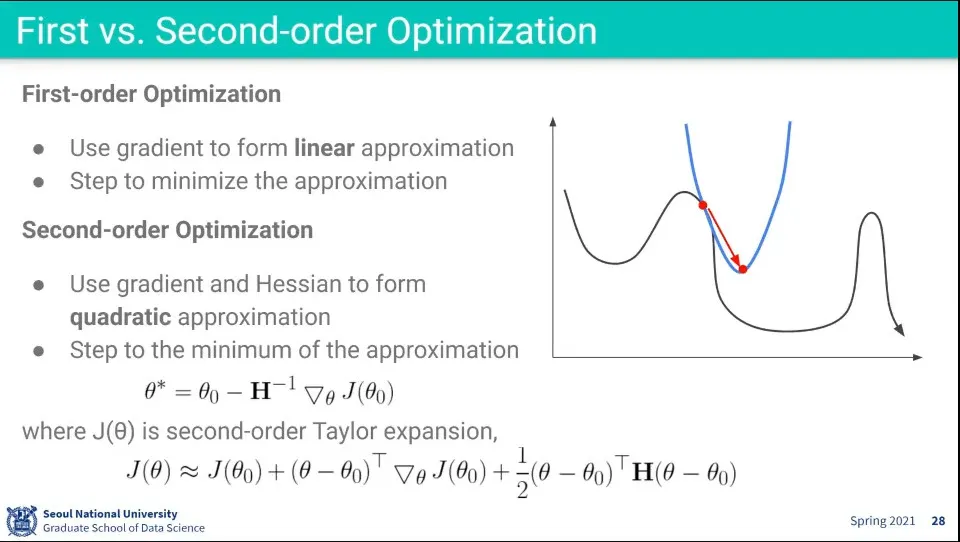
최적화를 2차식으로도 할 수 있다.
◦
2차식은 Talyor 전개를 이용함
•
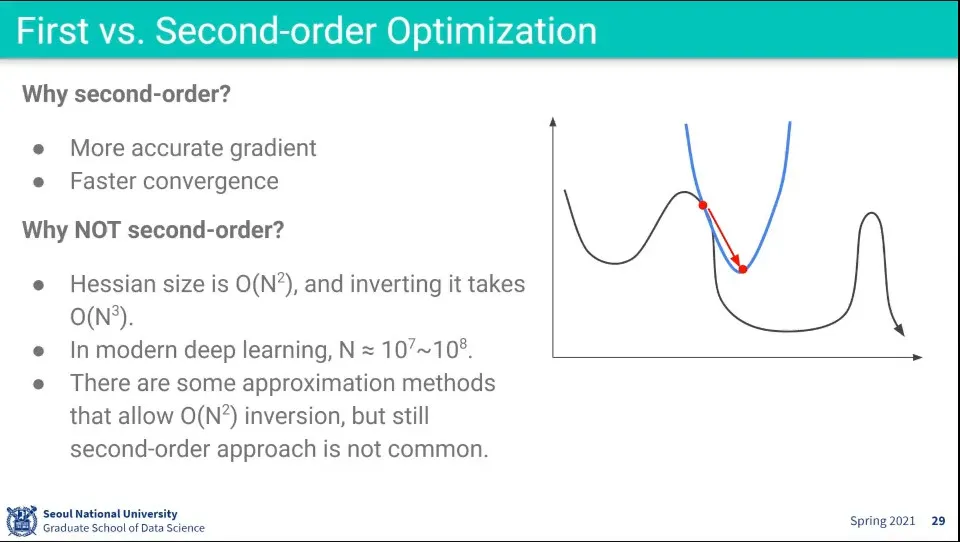
2차식을 이용하면 계산 횟수를 줄여서 최적점을 찾을 수 있음
◦
하지만 계산상 계산 시간이 의 형태라서 오래 걸리기 때문에 빠르다고 하기 어려움
•
일단 Adam으로 시작해라
•
그 다음에 SGD+Momentum을 적용해 봐라
•
Initial Learning rate는 모델과 데이터셋에 맞게 적용해야 함
•
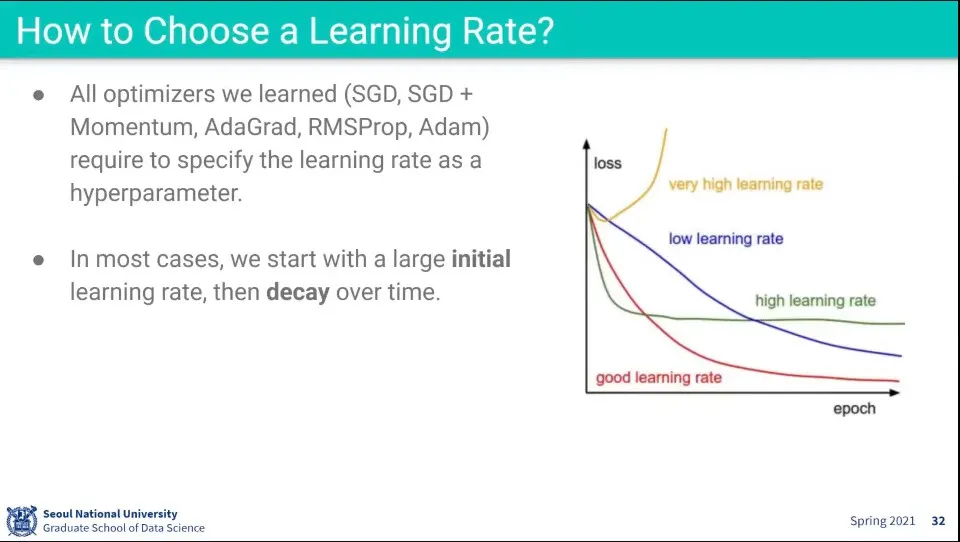
Learnig rate를 잘못 잡으면 발산할 수도 있음
•
일단 처음에는 큰 숫자를 쓰고, 시간에 따라 decay를 시키는게 일반적임
•
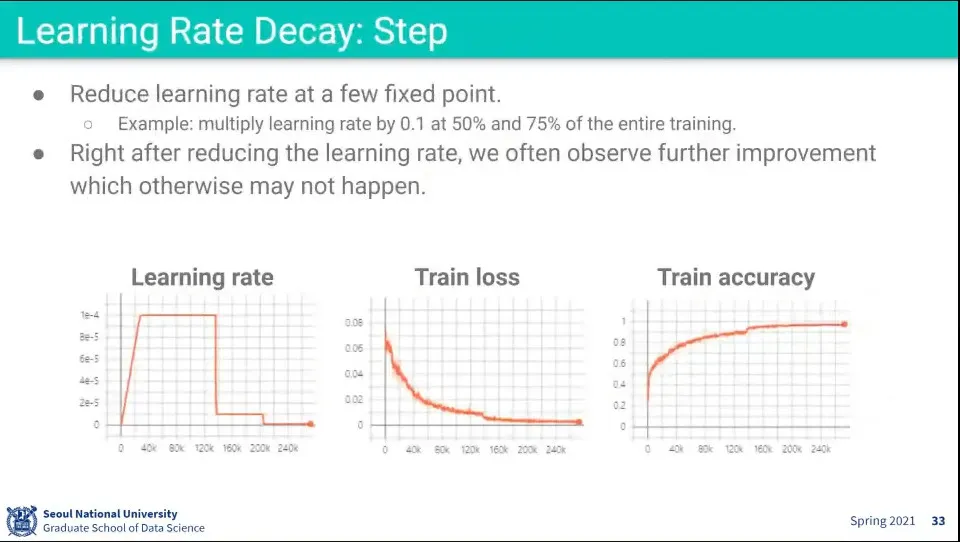
Learing rate decay 사례
◦
첫 번째는 warm up을 한 후에 learning rate를 크게 키웠다가 나중에 급격하게 decay 시킴
•
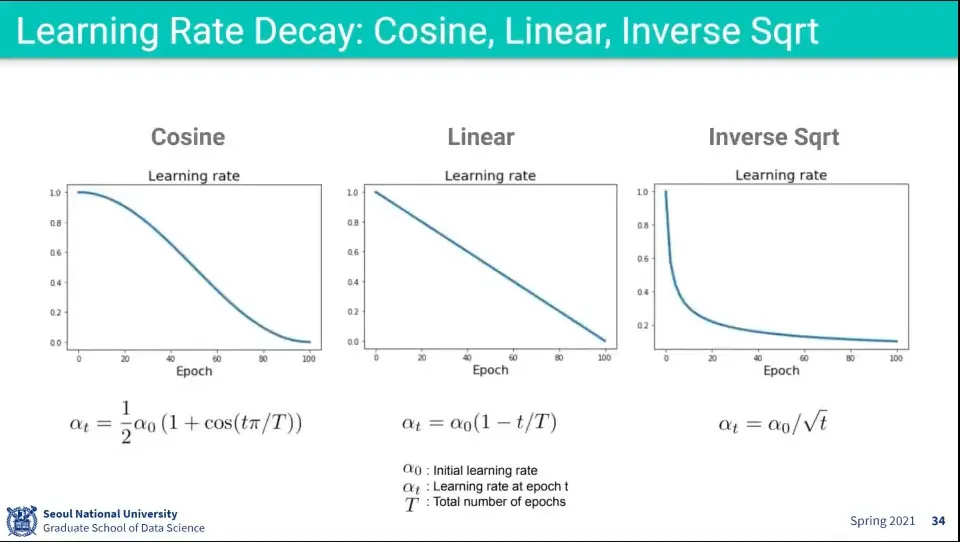
일반적으로 decay에 사용되는 방식들
◦
실험해 보고 결정하라
•
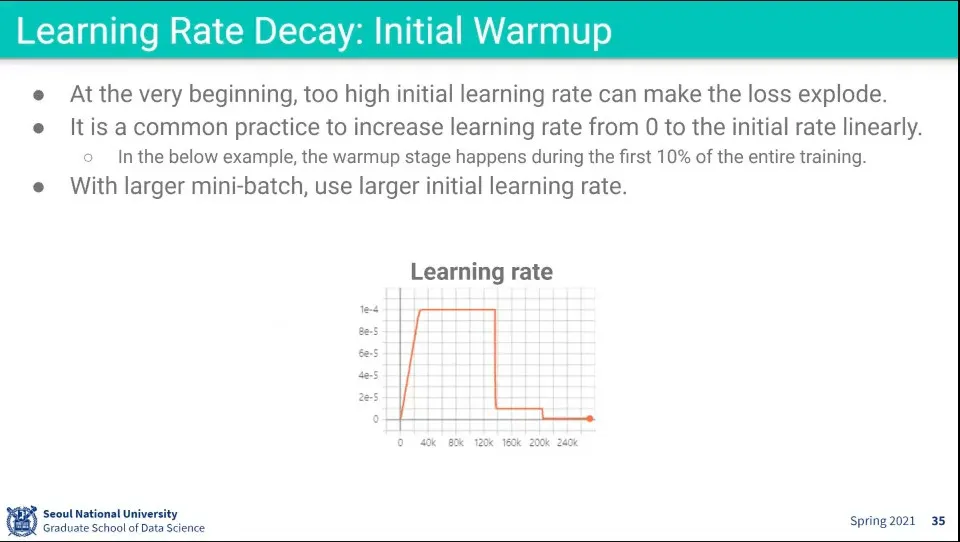
맨 처음에는 warm up으로 작게 시작해서 조금씩 키우는 방법을 사용함.
◦
처음부터 크게 하면 너무 뛰어 다닐 수 있으므로 작게 시작해서 조금씩 키워가며 warm up을 시킴
•
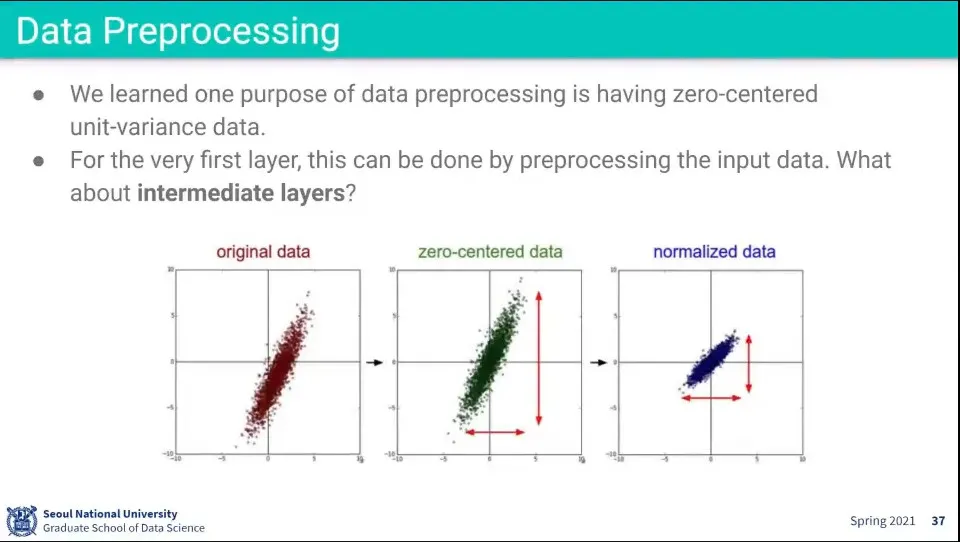
Data Preprocessing에서 zero-centered 와 nomalized를 적용함
◦
문제는 zero-centered는 처음 layer에는 잘 적용되었지만, 뒤의 layer로 넘어갈 수록 zero-centered가 안 될 수 있음
•
뒤의 layer들도 zero-centered가 되도록 하는게 batch normalization
◦
input에 대해 평균(기댓값)을 빼고 표준편차로 나눈다. -이건 normalization
•
데이터를 normalizatoin 할 평균(기댓값)과 표준편차는 미니배치에서 계산한다.
•
무작정 normalization 하면 값이 깨지기 때문에, 그것을 다시 원복할 수 있는 계산을 해줘야 함.
◦
위 식에서 는 normalization한 것이고
◦
이것을 다시 원복 시키기 위해 와 를 구해줘야 하는데 —이때 는 표준편차의 역할을 해줘야하고 는 평균(기댓값) 역할을 해줘야 함— 는 따로 구하지 않고 학습을 통해 배우도록 함.
◦
그러면 적당히 비슷한 값이 나오게 된다.
•
고로 batch normalization 할 때는 앞에 normalization 하는 것과 함께 뒤에 원복하는 것도 넣어줘야 한다.
•
테스트할 때는 평균과 표준편차를 구할 수 없기 때문에 학습할 때 값을 저장해 두었다가 사용해야 함.
•
Batch Normalization은 계산량은 복잡하지 않은데, 그 효과는 크기 때문에 표준처럼 사용 된다.
•
그런데 Batch normalization은 평균과 표준편차가 유사하다는 가정하에 돌아가는 방법인데, 모델을 학습 시키고 시간이 많이 지나면, 현시점의 테스트 데이터가 학습 시점의 데이터와 평균, 표준편차가 같다는 보장을 할 수가 없음
•
이를 보완하는게 Batch Renormalization
•
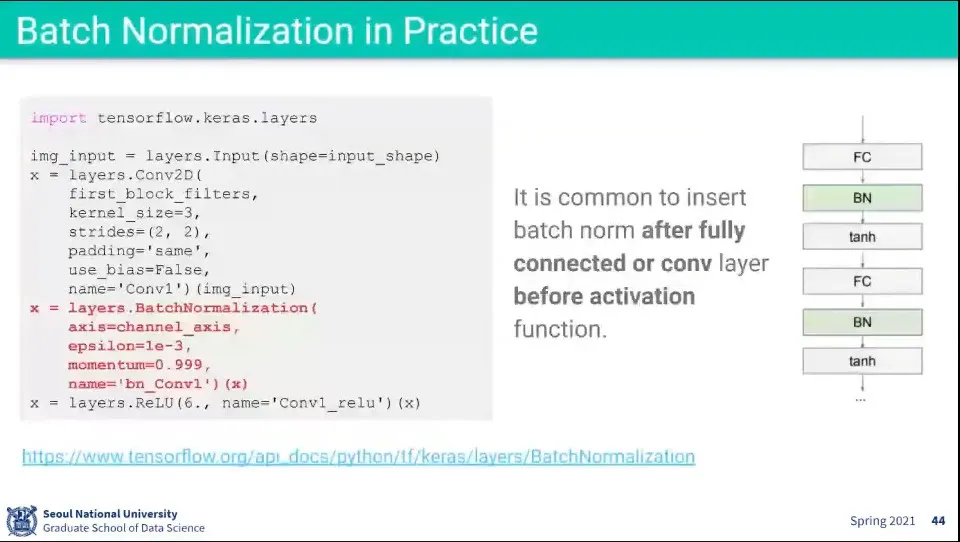
Batch Normalization 사용 예
◦
레이어를 추가해 주면 나머지는 프레임워크가 알아서 해준다.
◦
내부 모습은 오른쪽 플로우와 같음. 활성화 함수 전에 Batch Normalization Layer가 추가 됨
•
Batch Normalization을 응용하여 다양한 방식으로 Normalization 하는 방법들이 발표 됨
•
학습할 때, 데이터 특성이나 기타 상황을 고려하여 적절한 방법을 사용하면 된다.