Search
Duplicate

수학/ Hypothesis testing

Frequentist approach

•
빈도주의 통계에서 사용되는 가설 검정 방법은 null hypothesis significance testing(NHST)라 부른다. 이것의 기본 아이디어는 δ(D)=I(t(D)≥t∗)\delta(\mathcal{D}) = \mathbb{I}(t(\mathcal{D}) \ge t^*) 형식의 이항 결정 규칙(binary decision rule)을 정의하는 것이다.
◦
여기서 t(D)t(\mathcal{D})는 데이터로부터 유도된 어떤 스칼라 검정 통계량이고 t∗t^*는 critical value(임계 값)이다. 검정 통계량이 임계값을 넘어서면 널 가설을 reject 한다.
•
검정 통계에 사용할 수 있는 종류가 많지만 t-statistic이라 하는 단순한 예는 다음처럼 정의된다.
t(D)=xˉ−μσ^/Nt(\mathcal{D}) = {\bar{x} - \mu \over \hat{\sigma} / \sqrt{N}}
•
여기서 xˉ\bar{x}는 D\mathcal{D}의 경험적 평균이고, σ^\hat{\sigma}는 경험적 표준편차이고, NN은 표본 크기이고, μ\mu는 모집단(population) 평균이고 널 가설(종종 0)의 평균 값에 해당한다.
•
임계값 t∗t^*를 계산하기 위해 결정 절차의 type I error rate를 제어하는(즉, 널 가설이 사실일 때 널 가설을 실수로 거절할 확률) 유의 수준(significance level) α\alpha를(종종 0.05) 고른다.
◦
그 다음 널 가설이 주어졌을 때, 검정 통계량의 샘플링 분포에서 꼬리 확률이 유의 수준과 일치하는 값 t∗t^*을 찾는다.
p(t(D~)≥t∗∣H0)=αp(t(\tilde{\mathcal{D}}) \ge t^*|H_0) = \alpha
•
이 구성은 p(δ(D~)=1∣H0)=αp(\delta(\tilde{\mathcal{D}}) = 1|H_0) = \alpha를 보장한다.
•
t(D)t(\mathcal{D})를 t∗t^*와 비교하는 것보다 더 일반적인(그러나 동등하지 않은) 접근은 정의된 t(D)t(\mathcal{D})의 p-value를 계산하는 것이다. p<αp < \alpha이면 널 가설을 거절할 수 있다.
•
불행히 p-value와 NHST가 널리 사용됨에도 많은 문제가 있다. 아래 참조.

Bayesian approach

•
가설 검정에 대한 베이지안 접근은 2가지가 있는데, 하나는 Bayes factor를 사용해서 모델을 비교하는 것이고, 다른 하나는 파라미터 추정에 기반한다.

Model comparison approach

•
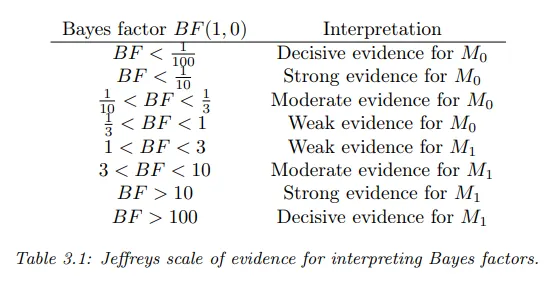
베이지안 가설 검정은 null hypothesis M0M_0과 alternative hypothesis M1M_1의 두 모델이 있는 베이지안 모델 선택의 특별한 경우이다. Bayes factor를 marginal likelihood의 비율로 정의하자.
B1,0≜p(D∣M1)p(D∣M0)=p(M1∣D)p(M0∣D)/p(M1)p(M0)B_{1,0} \triangleq {p(\mathcal{D}|M_1) \over p(\mathcal{D}|M_0)}= {p(M_1|\mathcal{D}) \over p(M_0|\mathcal{D})}/{p(M_1)\over p(M_0)}
•
이것은 다양한 복잡성의 모델을 비교할 수 있도록 파라미터를 적분하는 것을 제외하고 likelihood ratio와 같다.
◦
B1,0>1B_{1,0} > 1이면 모델 1을 선호하고 아니면 모델 0을 선호한다. 아래 표 참조.
•
그러나 베이지안 모델 선택에 대해 부당한(improper) prior(예: 적분해서 1이 되지 않는 prior 등)를 사용할 때 문제가 될 수 있기 때문에 주의해야 한다.

Parameter estimation approach

•
베이지안 가설 검정 접근은 marginal likelihood를 계산해야 하는 계산적 어려움과 prior에 대한 민감도와 같은 몇 가지 결점이 있다. 대안으로 일반적인 방법에서 모델의 파라미터를 추정한 다음에 널 가설에 해당하는 파라미터 값에 posterior 확률이 얼마나 할당되었는지를 보는 방법이 있다.
◦
예컨대 동전이 공정한지 테스트하려면, 우선 posterior p(θ∣D)p(\theta|\mathcal{D})를 계산한 다음에 p(0.5−ϵ<θ<0.5+ϵ∣D)p(0.5-\epsilon < \theta < 0.5+\epsilon|\mathcal{D})를 계산해서 널 가설의 타당함을 평가할 수 있다. 여기서 (0.5−ϵ,0.5+ϵ)(0.5-\epsilon, 0.5+\epsilon)은 region of practical equivalence(ROPE)라고 부른다.
◦
이것은 계산적으로 단순할 뿐만 아니라 그저 가설을 수락할지 거절할지 대신 효과 크기(즉 0.50.5의 널 값으로부터 θ\theta의 기대 편차)를 정량화 할수 있다. 이 접근은 Bayesian estimation이라고 부른다.
•
이것의 예는 다음과 같은 종류들이 있다.
◦
Binomial test
◦
χ2\chi^2 test
◦
t-test
◦
paired t-test
◦
two sample t-test
•
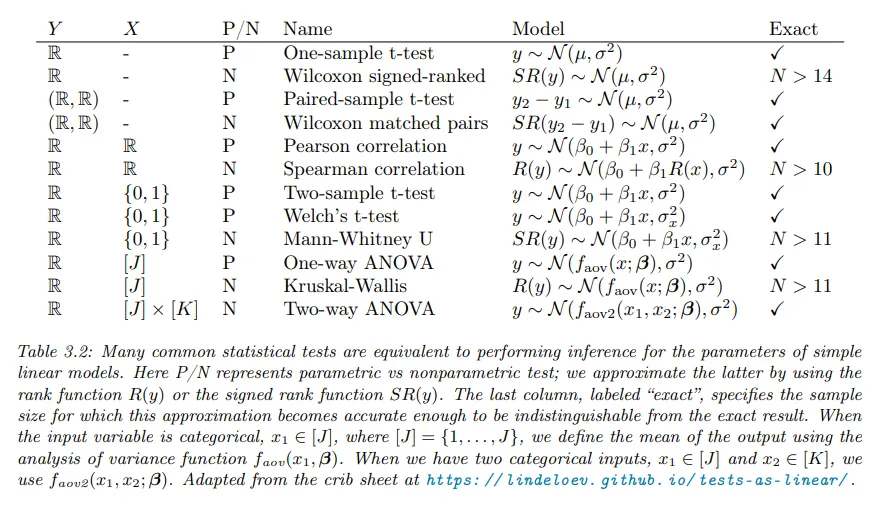
다행히 가장 일반적인 테스트 중 상당수가 일반화 선형 모델이나 GLM(Gaussian Linear Model)의 파라미터 추론으로 표현될 수 있다. 아래 표 참조.

Approximating nonparametric tests using the rank transform

•
가우시안이나 student 분포를 따르지 않는 데이터의 설정에 표준 테스트를 일반화하는 ‘nonparametric tests’를 사용하는 것이 일반적이다.
◦
이런 테스트를 근사하는 단순한 방법은 원본 데이터를 order statistics로 교체하고 표준 파라메트릭 테스트를 적용하는 것이다. 이렇게 하면 표본 크기 N≥10N \ge 10인 경우 표준 nonparametric 테스트에 좋은 근사를 얻을 수 있다.
•
구체적으로 데이터 포인트(스칼라라고 가정)가 정렬된 다음 순서대로 정수값으로 교체되는 rank transform을 계산할 수 있다.
◦
예컨대 D=(3.6,3.4,−5.0,8.2)\mathcal{D} = (3.6,3.4,-5.0,8.2)의 rank transform은 R(D)=(3,2,1,4)R(\mathcal{D}) = (3,2,1,4)이다.
•
대안으로 우선 절대값 크기로 값을 정렬하고 해당하는 부호를 붙이는 singed ranked를 사용할 수 있다.
◦
예컨대 D=(3.6,3.4,−5.0,8.2)\mathcal{D} = (3.6,3.4,-5.0,8.2)의 singed rank transform은 SR(D)=(2,1,−3,4)SR(\mathcal{D}) = (2,1,-3,4)이다.
•
이제 GLM(gaussian linear model) 같은 파라메트릭 모델을 rank-transformed 데이터로 쉽게 맞출 수 있다. 이에 대해 다음과 같은 테스트가 가능하다. (실제 예는 생략)
◦
t-test
◦
correlation test
◦
one-way ANOVA
◦
multi-way ANOVA
◦
χ2\chi^2 test

참고

Made with