Hierarchical Priors
•
베이지안 모델은 파라미터에 대해 prior 를 지정해야 한다. prior의 파라미터는 hyperparameter라 부르고 라 표기한다.
◦
하이퍼파라미터가 알려지지 않은 경우, 하이퍼파라미터에 prior 지정하면 hierarchical Bayesian model 또는 multi-level model를 정의할 수 있다. 이것을 로 표시한다.
◦
hyperparameter에 대한 prior는 고정되었다고 가정하면 (예: 최소화 informative prior를 사용) 결합 분포는 다음의 형식을 갖는다.
•
하이퍼파라미터 자체를 데이터포인트로 취급하여 하이퍼파라미터를 학습할 수 있기를 바란다.
•
이런 접근 방식이 적합한 일반적인 설정은 관련 데이터셋 가 있고 각각 자체 파라미터 가 있는 경우이다.
◦
각 그룹 에 대해 독립적으로 를 추론하면 가 작은 데이터셋인 경우(예: 조건 가 특성의 희소한 조합 또는 인구가 희소한 지역에 해당하는 경우) 좋지 않은 결과를 얻을 수 있다. 물론 모든 데이터를 모아 단일 모델 을 계산할 수 있지만 이렇게 하면 하위집단(subpopulation)을 모델링할 수 없다.
•
계층적 베이지안 모델은 데이터가 많은 그룹(따라서 정보가 풍부한 posterior )의 통계적 강점을 빌려서 데이터가 적은 그룹(따라서 불확실성이 높은 posterior )을 도울 수 있다.
◦
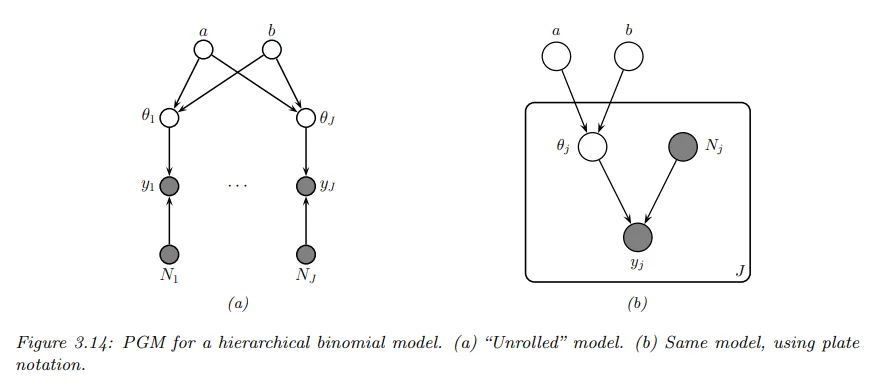
이 아이디어는 정보가 풍부한 그룹 가 에 대한 좋은 추정치를 가질 것이며, 이를 통해 를 추론할 수 있고, 이를 통해 데이터가 적은 그룹 의 를 추정하는데 도움을 줄 수 있다는 것이다. (아래 그림에 표시된 것처럼 숨겨진 공통 부모 노드 를 통해 정보가 공유된다.)
•
이런 모델을 피팅한 후에 posterior 예측 분포의 2가지 종류를 계산할 수 있다. 현재 그룹 에 대한 관찰을 예측하기 원한다면 다음을 사용해야 한다.
•
그러나 아직 측정되지 않았지만 현재 그룹과 로 비교 가능한(또는 교환 가능한) 새로운 그룹 *에 대한 관찰을 예측하기 원하면 다음을 사용해야 한다.