Search
Duplicate

수학/ Gaussian Joint Distributions

The multivariate normal

Definition

•
MVN 밀도는 다음처럼 정의된다.
N(x∣μ,Σ)≜1(2π)D/2∣Σ∣1/2exp⁡[−12(x−μ)⊤Σ−1(x−μ)]\mathcal{N}(\bold{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma}) \triangleq {1 \over (2\pi)^{D/2}|\boldsymbol{\Sigma}|^{1/2}} \exp \left[ -{1\over2} (\bold{x}-\boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1}(\bold{x}-\boldsymbol{\mu}) \right]
•
여기서 μ=E[x]∈RD\boldsymbol{\mu} = \mathbb{E}[\bold{x}] \in \mathbb{R}^D는 평균 벡터이고
◦
Σ=Cov[x]\boldsymbol{\Sigma} = \text{Cov}[\bold{x}]는 D×DD \times D 공분산 행렬이다.
◦
정규화 상수 Z=(2π)D/2∣Σ∣1/2Z = (2\pi)^{D/2}|\boldsymbol{\Sigma}|^{1/2}는 pdf 적분이 1이 되도록 하기 위한 것이다.
◦
지수 내부의 식(−0.5-0.5의 계수 무시)는 데이터 벡터 x\bold{x}와 평균 벡터 μ\boldsymbol{\mu} 사이의 제곱된 Mahalanobis 거리이다. 다음처럼 주어진다.
dΣ(x,μ)2=(x−μ)⊤Σ−1(x−μ)d_{\boldsymbol{\Sigma}}(\bold{x},\boldsymbol{\mu})^2 = (\bold{x}-\boldsymbol{\mu})^\top\boldsymbol{\Sigma}^{-1}(\bold{x}-\boldsymbol{\mu})

Gaussian shells

•
다변량 가우시안은 고차원에서 직관과 다르게 행동한다. 예컨대 x∼N(0,ID)\bold{x} \sim \mathcal{N}(\bold{0},\bold{I}_D)에서 샘플을 추출한다고 할 때, (여기서 DD는 차원의 수이다) x\bold{x}의 대부분이 어디에 있을지 예상할 수 있을까?
◦
pdf의 peak(mode)가 원점이기 때문에 대부분의 샘플이 원점 근처에 있다고 생각하는 것은 자연스럽지만 고차원에서 가우시안 집합의 일반적인 형태는 원점으로부터의 거리가 r=σDr = \sigma\sqrt{D}이고 두께(thickness)가 O(σD14)O(\sigma D^{1\over4})인 얇은 shell(껍데기) 또는 annulus(고리) 모양이다.
•
이것의 직관적인 이유는 다음과 같다.
◦
밀도는 원점으로부터 e−r2/2e^{-r^2/2}로 감소하지만 구(sphere)의 부피(volume)는 rDr^D로 증가한다. 질량은 밀도 곱하기 부피이므로 대부분의 점이 이 두 항이 ‘균형을 이루는’ 이 고리 안에 있게 된다.
◦
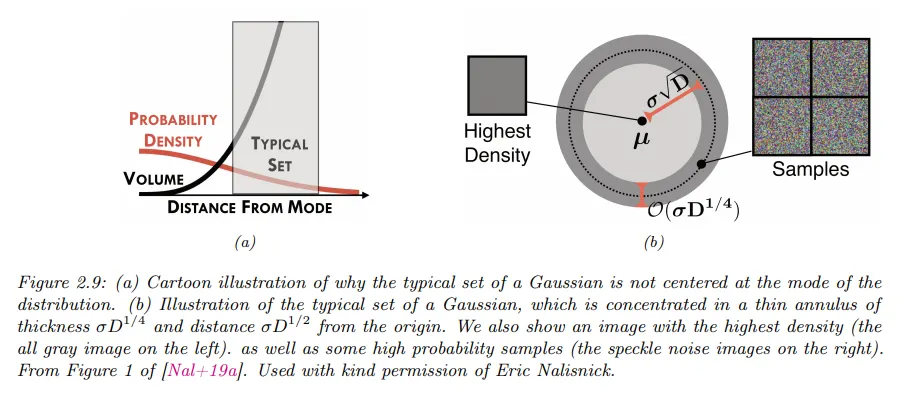
이를 ‘가우시안 비누 방울(Gaussian soap bubble)’ 현상이라고 하며, 아래 그림에 설명되어 있다.
•
가우시안에 대한 일반적인 집합이 왜 반경 D\sqrt{D}의 얇은 고리(annulus)에 모이는지 보기 위해 원점으로부터 점 x\bold{x}의 제곱 거리를 다음과 같이 생각하자.
◦
아래에서 xi∼N(0,1)x_i \sim \mathcal{N}(0,1)
d(x)=∑i=1Dxi2d(\bold{x}) = \sqrt{\sum_{i=1}^D x_i^2}
•
이에 대한 기대 제곱 거리와 분산 제곱 거리는 다음과 같이 주어진다.
E[d2]=∑i=1DE[xi2]=DV[d2]=∑i=1DV[xi2]=D\mathbb{E}[d^2] = \sum_{i=1}^D \mathbb{E}[x_i^2] = D \\ \mathbb{V}[d^2] = \sum_{i=1}^D \mathbb{V}[x_i^2] = D
•
DD(차원)가 커짐에 따라 변동 계수(coefficient of variation)는 0으로 간다.
lim⁡D→∞std[d2]E[d2]=lim⁡D→∞DD=0\lim_{D \to \infty} {\text{std}[d^2] \over \mathbb{E}[d^2]} = \lim_{D \to \infty}{\sqrt{D} \over D} = 0
•
따라서 기대 제곱 거리는 DD 주위에 모여들게 된다. 따라서 기대 거리는 E[d(x)]=D\mathbb{E}[d(\bold{x})] = \sqrt{D} 주위에 모여들게 된다.

Marginals and conditionals of an MVN

•
랜덤 변수 x\bold{x}의 벡터를 x1\bold{x}_1과 x2\bold{x}_2 2개의 부분으로 분할한다. 따라서
μ=(μ1μ2),Σ=(Σ11Σ12Σ21Σ22)\boldsymbol{\mu} = \begin{pmatrix} \boldsymbol{\mu}_1 \\ \boldsymbol{\mu}_2 \end{pmatrix}, \boldsymbol{\Sigma} = \begin{pmatrix} \boldsymbol{\Sigma}_{11} & \boldsymbol{\Sigma}_{12} \\ \boldsymbol{\Sigma}_{21} & \boldsymbol{\Sigma}_{22} \end{pmatrix}
•
이 분포의 marginal은 다음과 같이 주어짐을 보일 수 있다.
p(x1)=∫N(x∣μ,Σ)dx2≜N(x1∣μ1m,Σ1m)=N(x1∣μ1,Σ11)p(x2)=∫N(x∣μ,Σ)dx1≜N(x2∣μ2m,Σ2m)=N(x2∣μ2,Σ22)\begin{aligned} p(\bold{x}_1) &= \int \mathcal{N}(\bold{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma})d\bold{x}_2 \triangleq \mathcal{N}(\bold{x}_1|\boldsymbol{\mu}_1^m, \boldsymbol{\Sigma}_1^m) = \mathcal{N}(\bold{x}_1|\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_{11}) \\ p(\bold{x}_2) &= \int \mathcal{N}(\bold{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma})d\bold{x}_1 \triangleq \mathcal{N}(\bold{x}_2|\boldsymbol{\mu}_2^m, \boldsymbol{\Sigma}_2^m) = \mathcal{N}(\bold{x}_2|\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_{22}) \end{aligned}
•
조건부 분포는 다음의 형식을 가짐을 보일 수 있다.
p(x1∣x2)=(x1∣μ1∣2c,Σ1∣2c)=N(x1∣μ1+Σ12Σ22−1(x2−μ2),Σ11−Σ12Σ22−1Σ21)p(x2∣x1)=(x2∣μ2∣1c,Σ2∣1c)=N(x2∣μ2+Σ21Σ11−1(x1−μ1),Σ22−Σ21Σ11−1Σ12)(2.78-79)\begin{aligned} p(\bold{x}_1|\bold{x}_2) &= (\bold{x}_1|\boldsymbol{\mu}_{1|2}^c, \boldsymbol{\Sigma}_{1|2}^c) = \mathcal{N}(\bold{x}_1|\boldsymbol{\mu}_1 + \boldsymbol{\Sigma}_{12}\boldsymbol{\Sigma}_{22}^{-1}(\bold{x}_2 - \boldsymbol{\mu}_2), \boldsymbol{\Sigma}_{11} - \boldsymbol{\Sigma}_{12}\boldsymbol{\Sigma}_{22}^{-1}\boldsymbol{\Sigma}_{21}) \\ p(\bold{x}_2|\bold{x}_1) &= (\bold{x}_2|\boldsymbol{\mu}_{2|1}^c, \boldsymbol{\Sigma}_{2|1}^c) = \mathcal{N}(\bold{x}_2|\boldsymbol{\mu}_2 + \boldsymbol{\Sigma}_{21}\boldsymbol{\Sigma}_{11}^{-1}(\bold{x}_1 - \boldsymbol{\mu}_1), \boldsymbol{\Sigma}_{22} - \boldsymbol{\Sigma}_{21}\boldsymbol{\Sigma}_{11}^{-1}\boldsymbol{\Sigma}_{12})\end{aligned}\\ \tag{2.78-79}
•
p(x1∣x2)p(\bold{x}_1|\bold{x}_2)의 posterior 평균이 x2\bold{x}_2의 선형 함수임에 유의하라. 그러나 posterior 공분산은 x2\bold{x}_2에 독립이다. 이것은 가우시안 분포의 기이한(peculiar) 속성이다.

Information (canonical) form

•
평균 벡터 μ\boldsymbol{\mu}와 공분산 행렬 Σ\boldsymbol{\Sigma}의 측면에서 MVN을 파라미터화하는 것이 일반적이다. 그러나 canonical(표준) parameter 또는 natural(자연) parameter를 사용하여 가우시안 분포를 표현하는 것이 유용할 수 있다. 다음처럼 정의한다.
Λ≜Σ−1,η≜Σ−1μ\boldsymbol{\Lambda} \triangleq \boldsymbol{\Sigma}^{-1}, \boldsymbol{\eta} \triangleq \boldsymbol{\Sigma}^{-1}\boldsymbol{\mu}
•
행렬 Λ=Σ−1\boldsymbol{\Lambda} = \boldsymbol{\Sigma}^{-1}은 정밀도(precision) 행렬이라 하고, 벡터 η\boldsymbol{\eta}는 precision-weighted 평균이라 한다.
•
다음을 사용하여 더 친숙한 moment 파라미터로 다시 변환할 수 있다.
μ=Λ−1η,Σ=Λ−1\boldsymbol{\mu} = \boldsymbol{\Lambda}^{-1}\boldsymbol{\eta}, \boldsymbol{\Sigma} = \boldsymbol{\Lambda}^{-1}
•
따라서 MVN을 다음처럼 canonical form으로(또는 information form이라고 한다) 작성할 수 있다.
Nc(x∣η,Λ)≜cexp⁡(x⊤η−12x⊤Λx)c≜exp⁡(−12η⊤Λ−1η)(2π)D/2det⁡(Λ−1)\begin{aligned} \mathcal{N}_c(\bold{x}|\boldsymbol{\eta},\boldsymbol{\Lambda}) &\triangleq c \exp\left( \bold{x}^\top \boldsymbol{\eta} - {1\over2}\bold{x}^\top\boldsymbol{\Lambda}\bold{x} \right) \\ c &\triangleq {\exp(-{1\over2}\boldsymbol{\eta}^\top \boldsymbol{\Lambda}^{-1}\boldsymbol{\eta}) \over (2\pi)^{D/2}\sqrt{\det(\boldsymbol{\Lambda}^{-1})}} \end{aligned}
•
여기서 표준 파라미터화 된 N()\mathcal{N}()와 구분하기 위해 Nc()\mathcal{N}_c() 표기법을 사용했다.
•
information 형식에서 marginalization과 conditioning 공식을 유도하는 것도 가능하다. marginal에 대해 다음이 성립한다.
p(x1)=Nc(x1∣η1m,Λ1m)=Nc(x1∣η1−Λ12Λ22−1η2,Λ11−Λ12Λ22−1Λ21)p(x2)=Nc(x2∣η2m,Λ2m)=Nc(x2∣η2−Λ21Λ11−1η1,Λ22−Λ21Λ11−1Λ12)(2.84-85)\begin{aligned} p(\bold{x}_1) &= \mathcal{N}_c(\bold{x}_1|\boldsymbol{\eta}_1^m, \boldsymbol{\Lambda}_{1}^m) = \mathcal{N}_c(\bold{x}_1|\boldsymbol{\eta}_1 - \boldsymbol{\Lambda}_{12}\boldsymbol{\Lambda}_{22}^{-1}\boldsymbol{\eta}_{2},\boldsymbol{\Lambda}_{11}-\boldsymbol{\Lambda}_{12}\boldsymbol{\Lambda}_{22}^{-1}\boldsymbol{\Lambda}_{21}) \\ p(\bold{x}_2) &= \mathcal{N}_c(\bold{x}_2|\boldsymbol{\eta}_2^m, \boldsymbol{\Lambda}_{2}^m) = \mathcal{N}_c(\bold{x}_2|\boldsymbol{\eta}_2 - \boldsymbol{\Lambda}_{21}\boldsymbol{\Lambda}_{11}^{-1}\boldsymbol{\eta}_{1},\boldsymbol{\Lambda}_{22}-\boldsymbol{\Lambda}_{21}\boldsymbol{\Lambda}_{11}^{-1}\boldsymbol{\Lambda}_{12})\end{aligned} \\ \tag{2.84-85}
•
조건부에 대해 다음이 성립한다.
p(x1∣x2)=Nc(x1∣η1∣2c,Λ1∣2c)=Nc(x1∣η1−Λ12x2,Λ11)p(x2∣x1)=Nc(x2∣η2∣1c,Λ2∣1c)=Nc(x2∣η2−Λ21x1,Λ22)\begin{aligned} p(\bold{x}_1|\bold{x}_2) &= \mathcal{N}_c(\bold{x}_1|\boldsymbol{\eta}_{1|2}^c, \boldsymbol{\Lambda}_{1|2}^c) = \mathcal{N}_c(\bold{x}_1|\boldsymbol{\eta}_1 - \boldsymbol{\Lambda}_{12}\bold{x}_2,\boldsymbol{\Lambda}_{11}) \\ p(\bold{x}_2|\bold{x}_1) &= \mathcal{N}_c(\bold{x}_2|\boldsymbol{\eta}_{2|1}^c, \boldsymbol{\Lambda}_{2|1}^c) = \mathcal{N}_c(\bold{x}_2|\boldsymbol{\eta}_2 - \boldsymbol{\Lambda}_{21}\bold{x}_1,\boldsymbol{\Lambda}_{22}) \end{aligned}
•
고로 moment 형식에서는 marginalization이 더 쉽고, information 형식에서는 conditioning이 더 쉽다는 것을 알 수 있다.

참조

Made with