Search
Duplicate

AI/ Vanishing Points and Lines

Point at Infinity

2d에서 직선 ax+by+c=0ax + by + c = 0은 homogeneous 벡터를 이용해서 다음과 같이 표현 가능하다.
ℓ=[abc]\ell = \begin{bmatrix} a \\ b \\ c \end{bmatrix}
여기서 −ab-{a\over b}는 slope(기울기)에 해당하고, −ca-{c\over a}는 xx-절편, −cb-{c\over b}는 yy-절편이 된다.
형식적으로 2d 직선은 다음처럼 정의된다.
∀p=[xy]∈ℓ,[abc][xy1]=0\forall p = \begin{bmatrix}x \\ y \end{bmatrix} \in \ell, \begin{bmatrix}a & b & c \end{bmatrix}\begin{bmatrix}x \\ y \\ 1 \end{bmatrix} = 0
일반적으로 두 직선 ℓ\ell과 ℓ′\ell'은 점 pp에서 교차하며, 이 점은 ℓ\ell과 ℓ′\ell' 사이의 cross product로 정의된다.
일반적으로 평행선은 교차하지 않는다고 하지만, 이 선들이 무한대에서 교차한다고 생각할 수 있다. homogeneous 좌표에서 무한대의 점은 [xy0]⊤[x \quad y \quad 0]^\top로 작성된다. 유클리드 좌표는 모든 좌표를 마지막 좌표로 나누어 얻을 수 있고, 여기서 마지막 좌표가 00이므로 무한대의 점이 된다. 따라서 homogeneous 좌표는 평행선의 경우에서도 교차를 정의하는 좋은 형식이다.
두 평행선 ℓ\ell과 ℓ′\ell'에 대해 두 직선의 기울기가 동일하므로 ab=a′b′{a \over b} = {a' \over b'}가 된다. homogeneous 좌표를 사용하여 교차점을 계산하면 다음을 확인할 수 있다. 아래서 i,j,k\bold{i}, \bold{j}, \bold{k}는 x,y,zx, y, z축의 단위 벡터이다.
ℓ×ℓ′=∣ijkabca′b′c′∣=[bc′−b′cca′−c′aab′−a′b]∝[b−a0]=x∞\begin{aligned} \ell \times \ell' &= \left| \begin{matrix} \bold{i} & \bold{j} & \bold{k} \\ a & b & c \\ a' & b' & c' \end{matrix} \right| = \begin{bmatrix} bc' - b'c \\ ca' - c'a \\ ab' - a'b \end{bmatrix} \propto \begin{bmatrix}b \\ -a \\ 0 \end{bmatrix} = x_\infty \end{aligned}
두 평행선이 무한대에서 교차한다는 것을 다시 확인할 수 있다. 두 평행선의 무한대에서의 교차점을 ideal point라고 부른다. 무한대의 점에 대해 흥미로운 속성은 동일한 slope −ab-{a\over b}를 갖는 모든 평행선이 ideal point를 통과한다는 것이다.
ℓ⊤x∞=[abc][b−a0]=0\ell^\top x_\infty = \begin{bmatrix}a & b & c \end{bmatrix} \begin{bmatrix}b \\ -a \\ 0 \end{bmatrix} = 0
무한대의 점 p∞p_\infty에 projective transform HH을 적용하면 다음과 같은 결과를 얻을 수 있다.
p′=Hp∞=[Atvb][110]=[px′py′pz′]p' = Hp_\infty = \begin{bmatrix}A & t \\ v & b \end{bmatrix} \begin{bmatrix}1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} p_x' \\ p_y' \\ p_z' \end{bmatrix}
p′p'의 마지막 요소가 non-zero이므로 이것은 무한대의 점이 아니다. 따라서 projective transformation은 무한대의 점을 무한대가 아닌 점에 매핑한다.
반면 무한대의 점 p∞p_\infty에 affine transformation HH을 적용하면 다음과 같이 무한대의 점을 얻는다.
p′=Hp∞=[At01][110]=[px′py′0]p' = Hp_\infty = \begin{bmatrix}A & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix}1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} p_x' \\ p_y' \\ 0 \end{bmatrix}

Line at Infinity

무한대의 점의 개념을 확장하여 무한대의 선을 정의할 수 있다. 2개 이상의 평행선 쌍을 고려하자. 각 평행선의 쌍은 무한대에서 한 점 {x∞,1,...,x∞,n}\{x_{\infty, 1}, ..., x_{\infty, n}\}에서 교차한다. 이 무한대의 모든 점을 지나는 직선 ℓ∞\ell_\infty (아래 그림에서 파란 선)는 ∀i,ℓ∞⊤x∞,i=0\forall i, \ell_\infty^\top x_{\infty, i} = 0를 만족해야 한다. 이것은 ℓ∞=[00c]⊤\ell_\infty = [0 \quad 0 \quad c]^\top를 의미한다. cc가 임의의 값이므로 ℓ∞=[001]⊤\ell_\infty = [0 \quad 0 \quad 1]^\top로 단순화할 수 있다.
무한대에서 점에 대한 관찰과 유사하게 무한대에서 직선에 대한 projective transformation은 무한대가 아닌 직선에 매핑될 수 있다. 반면 affine transformation은 무한대의 직선을 무한대의 직선으로 매핑한다.

Vanishing Point

3d 세계에서 평면의 방정식은 ax1+bx2+cx3+d=0ax_1 + bx_2 + cx_3 + d = 0이 되며, 이는 다음과 같이 작성할 수 있다.
x⊤[abcd]=ax1+bx2+cx3+d=0x^\top \begin{bmatrix}a\\b\\c\\d \end{bmatrix} = ax_1 + bx_2 + cx_3 + d = 0
여기서 (a,b,c)(a, b, c)는 해당 평면에 수직인 normal 벡터이고 dd는 normal 벡터의 방향에서 원점에서 평면까지의 거리에 해당한다. normal 벡터는 평면의 기울기와 방향을 정의한다.
3d에서 직선은 두 평면의 교차로 정의되는데, 4개의 자유도를 갖기 때문에 간편하게 표현하기 어렵다. 그러나 3d에서 점은 2d에서와 유사하게 정의 가능하며, 3d에서 무한대의 점은 3d에서 평행선의 교차점으로 정의된다. 평행선은 동일 평면 내에서 만나지 않는 선이라는 점에 주의하라. 동일한 평면에 존재하지 않으면서 교차하지 않는 선은 꼬인선(skew lines)이라고 한다.
3d에서 무한대의 점 x∞x_\infty에 projective transformation을 적용하면 homogeneous 좌표에서 무한대가 아닌 이미지 평면에서 점 x∞x_\infty을 얻을 수 있는데, 이 점을 vanishing point(소실점)이라고 한다.
3d에서 평행선, 이미지 대응 vanishing point, 카메라 파라미터 K,R,TK, R, T 사이의 유용한 관계를 유도할 수 있다. 카메라 reference system에서 3d 평행선의 집합의 방향을 d=(a,b,c)d = (a, b, c)라 정의하자. 이 직선들은 무한대의 한 점에서 교차하고 그 점을 카메라 행렬 KK를 이용하여 이미지에 projection하면 다음처럼 정의되는 vanishing point vv가 된다.
v=Kd=[α0cx0βcy001][abc]=[αa+cxcβb+cycc]v = Kd = \begin{bmatrix} \alpha & 0 & c_x \\ 0 & \beta & c_y \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} a \\ b \\ c \end{bmatrix} = \begin{bmatrix} \alpha a + c_xc \\ \beta b + c_yc \\ c \end{bmatrix}
위 결과를 동차좌표로 정규화하여 실제 소실점을 구한다.
vnormalized=(αa+cxcc,βb+cycc,1)v_\text{normalized} = \left({\alpha a + c_xc \over c}, {\beta b + c_yc \over c}, 1 \right)
위 방정식을 dd에 대해 정리하고 정규화하여 다음을 얻을 수 있다.
d=K−1v∥K−1v∥d = {K^{-1} v\over \|K^{-1}v\|}

Vanishing Line(Horizon line)

평면 Π\Pi를 평행선의 superset이라 하면, 각 평행선의 집합은 무한대에서 한 점에서 교차한다. 이러한 무한대의 점들의 집합을 지나는 직선이 Π\Pi와 연관된 무한대의 선 ℓ∞\ell_\infty이다. 무한대에서 직선은 또한 두 평행 평면이 교차하는 선으로 정의될 수 있다.
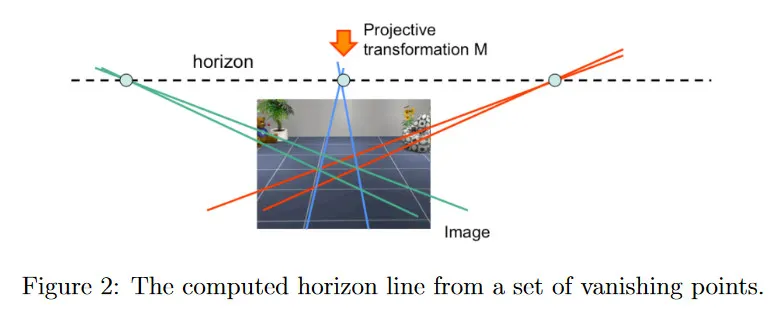
ℓ∞\ell_\infty를 이미지 평면으로 projective transformation하면 더는 무한대의 선이 아니며, 이를 vanishing line(소실선) 또는 horizon line(수평선) ℓhoriz\ell_\text{horiz}라 부른다. horizon line은 이미지의 대응점 vanishing point를 지나는 선이다. horizon line을 다음처럼 계산할 수 있다.
ℓhoriz=HP−⊤ℓ∞\ell_\text{horiz} = H_P^{-\top}\ell_\infty
horizon line의 개념을 통해 수학적으로 쉽게 드러나지 않는 이미지의 속성을 직관적으로 추론할 수 있다. 예컨대 아래 그림에서 지면의 선들이 이미지 좌표에서 평행이 아니지만, 그 선들이 3d 세계에서 평행하다는 것을 이해할 수 있다.
이미지 내의 모든 평행 선은 대응하는 vanishing point를 갖고, 이미지 내의 모든 평행 면은 대응하는 vanishing line(horizon line)을 갖는다. 모든 선에 대해 임의로 평행한 선을 만들 수 있고, 모든 면에 대해 임의로 평행한 면을 만들 수 있기 때문에 실제적으로 모든 선과 모든 면은 해당하는 vanishing point와 vanishing line을 갖는다고 할 수 있다. 다만 해당 vanishing point와 vanishing line은 위 이미지와 같이 이미지 내에 존재할 수도 있고 이미지 밖에 존재할 수도 있음.
추가로 3d 평면의 normal nn과 해당하는 평면의 horizon line ℓhoriz\ell_\text{horiz} 사이에 다음의 관계가 존재한다.
n=K⊤ℓhorizn = K^\top \ell_\text{horiz}
이것은 평면과 연관된 horizon line을 인식할 수 있고 카메라가 calibration 되어 있으면 그 평면의 orientation을 추정할 수 있다는 뜻이다.

평행선 사이의 각도

3d에서 두 쌍의 평행선이 방향 d1d_1과 d2d_2를 가지고 무한대의 점 x1,∞x_{1,\infty}와 x2,∞x_{2,\infty}와 연관되어 있고, 해당하는 vanishing point가 v1v_1와 v2v_2라 하자. 이때 두 평행선 사이의 각도를 아래처럼 두 평행선의 방향 d1d_1과 d2d_2에 대해 cosine 규칙을 사용하여 구할 수 있다. 여기서 방향 d1d_1과 d2d_2는 해당하는 vanishing point v1v_1와 v2v_2와 카메라 intrinsic를 이용하여 구할 수 있다.
cos⁡θ=d1⋅d2∥d1∥∥d2∥=v1⊤ωv2v1⊤ωv1v2⊤ωv2\begin{aligned} \cos \theta &= {d_1 \cdot d_2 \over \|d_1\|\|d_2\|}\\ &= {v_1^\top \omega v_2 \over \sqrt{v_1^\top \omega v_1} \sqrt{v_2^\top \omega v_2}} \end{aligned}
여기서 ω=(KK⊤)−1\omega = (KK^\top)^{-1}

평행면 사이의 각도

평행선 사이의 각도를 평면 사이의 각도로 확장할 수 있다. 두 평면 사이의 각도 θ\theta는 아래와 같이 두 평면의 normal 벡터 n1n_1과 n2n_2에 대해 cosine 규칙을 사용하여 구할 수 있다. 여기서 normal 벡터 n1n_1과 n2n_2는 해당하는 horizon line ℓ1\ell_1과 ℓ2\ell_2과 카메라 intrinsic를 이용하여 구할 수 있다.
cos⁡θ=n1⋅n2∥n1∥∥n2∥=ℓ1⊤ω−1ℓ2ℓ1⊤ω−1ℓ1ℓ2⊤ω−1ℓ2\begin{aligned} \cos \theta &= {n_1 \cdot n_2 \over \|n_1\|\|n_2\|}\\ &= {\ell_1^\top \omega^{-1}\ell_2 \over \sqrt{\ell_1^\top \omega^{-1} \ell_1} \sqrt{\ell_2^\top \omega^{-1} \ell_2}} \end{aligned}

참고

Made with