Epipolar Geometry
epipolar geometry에서는 동일한 3d 점 를 관찰하는 2대의 카메라가 포함된다. 아래 그림 참조.
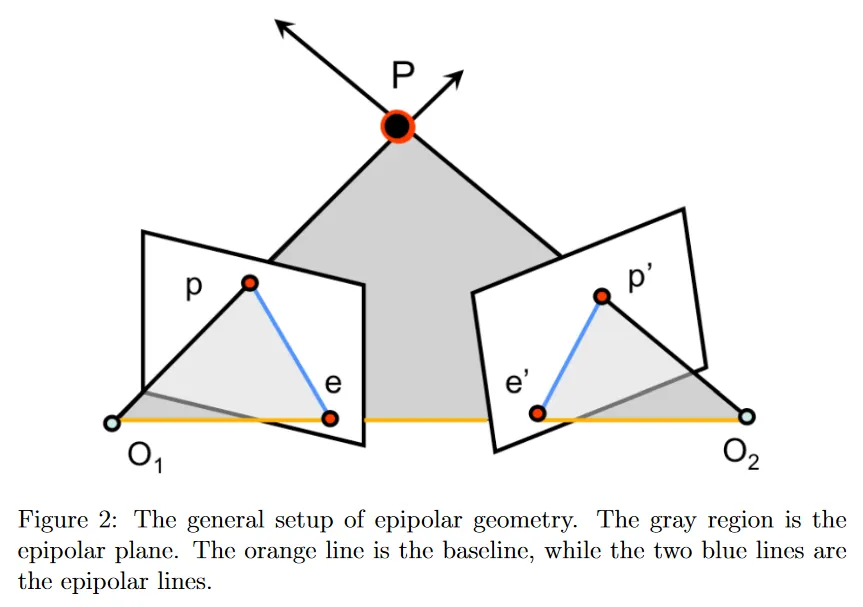
각 이미지 평면에서 의 투영은 가 된다. 두 카메라 중심은 이고 과 사이의 직선을 baseline이라 부른다.
두 카메라의 중심과 에 의해 정의되는 평면을 epipolar plane이라 부른다이는 아래 그림의 회색 영역으로 표시되는데, 이미지 상에는 삼각형으로 표현되었지만, 두 카메라의 중심 와 을 모두 포함하는 평면이라고 이해하는 편이 낫다.
baseline이 두 이미지 평면과 교차하는 지점 를 epipole이라 한다. 이것은 두 카메라의 중심을 상대의 이미지 평면에 투영한 점을 의미한다. epipole은 3d 점 와 무관하게 고정된 위치에 존재한다.
epipolar plane과 두 이미지 평면이 교차하는 선을 epipolar line이라 부른다. 이것은 이미지 평면 상의 투영점 과 이미지 평면과 baseline의 교차점 (epipole) 를 연결하는 선이 된다. 따라서 이미지 상의 모든 epipolar line은 항상 epipole을 지난다.
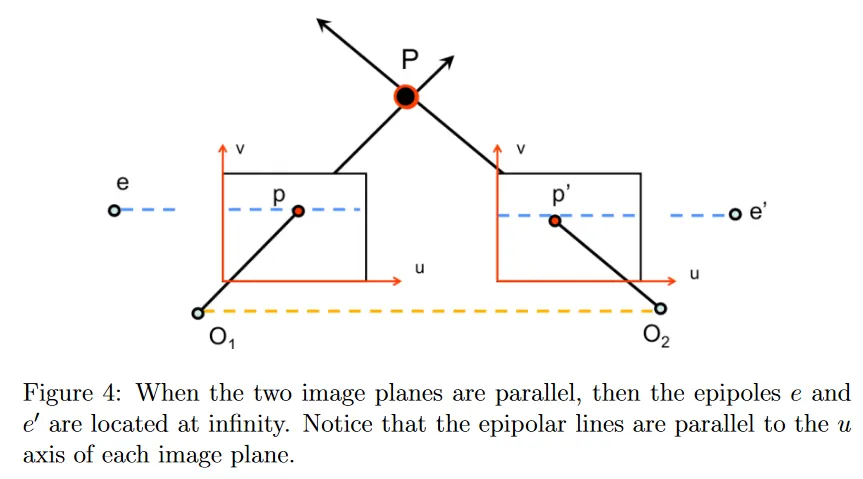
두 이미지 평면이 서로 평행하면 흥미로운 상황이 발생한다. 이미지 평면이 서로 평행하면 를 결합하는 baseline이 이미지 평면과 평행하기 때문에 epipole 와 는 무한대에 위치하고, 따라서 의 투영 와 epipole 를 잇는 epipolar line은 를 지나는 수평선이 된다.
이 경우의 또 다른 중요한 부산물은 epipolar line이 각 이미지 평면의 축과 평행하다는 것이다. 이 경우는 rectification에 특히 유용하다.
현실에서 3d 점의 위치 는 주어지지 않지만, 이미지 평면에 투영된 점 를 알고, 카메라 위치 를 알기 때문에, epipolar plane을 정의할 수 있다. 그러면 이 epipolar plane을 사용하여 epipolar line을 결정할 수 있다. 정의에 따라 의 두 번째 이미지에 대한 투영 는 반드시 두 번째 이미지의 epipolar line 상에 위치해야 한다. 따라서 epipolar geometry를 통해 이미지 쌍 사이의 강력한 제약 조건을 만들 수 있다.