•
이전에 들었던 유사한 부분이 많기 때문에 간략히 정리. 상세 내용은 아래 페이지 참조
•
머신러닝은 Data-Driven 접근 방식이다.
•
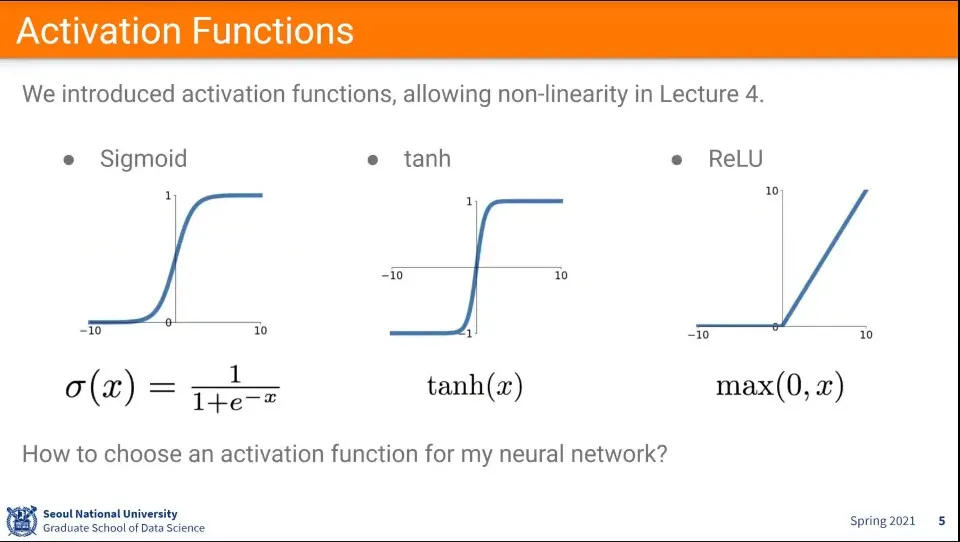
활성화 함수에는 Sigmoid, tanh, ReLU를 많이 사용한다.
•
Sigmoid는 처음에 많이 썼었고, 작은 네트워크에서는 잘 동작 함
•
그러나 Deep Neural Network 시대가 오면서 아래와 같은 이유로 잘 안 쓰임.
◦
gradient를 죽임
◦
zero가 center가 아님
◦
exp 연산이 비쌈
•
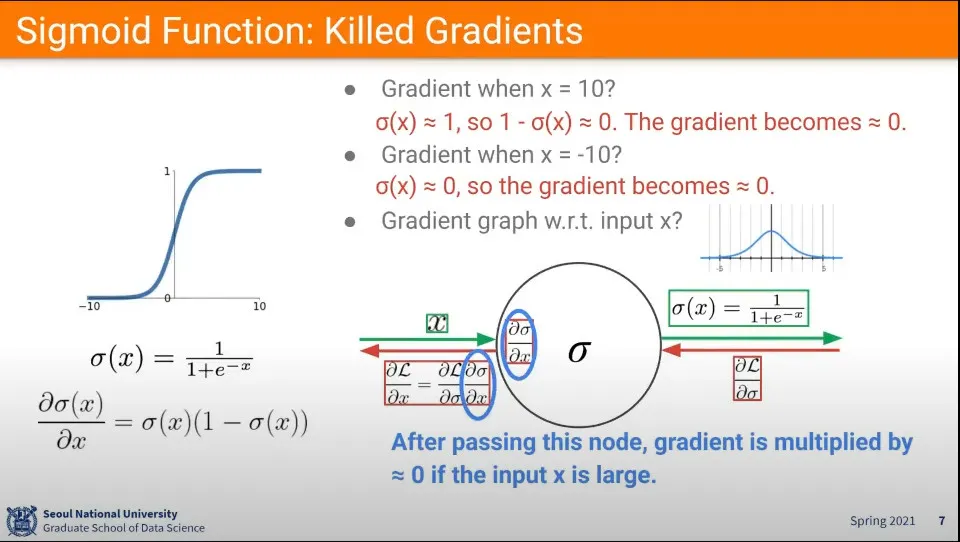
시그모이드 함수에서 input이 5이상의 큰 값이 들어오면 gradient가 0이 되게 됨.
◦
(이미지 중간의 분포도 참고, -5 ~ 5 사이의 분포는 적절한 값을 갖지만 그 범위를 벗어나게 되면 0에 가까운 값이 나옴)
◦
엄밀히 말해 0에 가까운 값이 되지만 layer가 겹겹이 쌓여 있기 때문에 layer를 지나가면서 점점 0으로 수렴하게 됨.
◦
때문에 layer를 점점 지나면서 학습이 이루어지지 않음
•
sigmoid가 0-1 사이의 양수만 나오기 때문에 학습이 항상 양수 방향으로만 진행이 됨
◦
오른쪽 아래 그래프와 같이 최적점이 우하향하는 경우 (파란 화살표) 학습은 우하향하는 방향으로 못가고 (+, +), (-, -)를 반복해서 학습이 됨 (빨간 화살표)
◦
비효율적인 상황 발생
•
비효율적인 문제이므로 앞의 gradient를 죽이는 것보다는 덜 치명적인 문제
•
sigmoid의 zero centered를 개선한 것이 Tanh
◦
하지만 근본적으로 sigmoid의 변형이기 때문에 killing gradient 문제를 해결하지 못함
•
Killing gradient를 해결한 것이 ReLU
•
하지만 zero-centered 문제는 다시 발생 함
•
ReLU의 문제를 개선해서 음수일 때 아주 작은 값을 사용하는 Leaky ReLU 방법이 나옴
•
ReLU에서 zero-centered를 개선한 함수.
•
그러나 exp 연산이 비싸다
•
그냥 ReLU를 써라
•
그 후에 최적화를 위해 Leaky ReLU나 ELU를 쓸 수 있다.
•
sigmoid나 tanh는 쓰지 마라
•
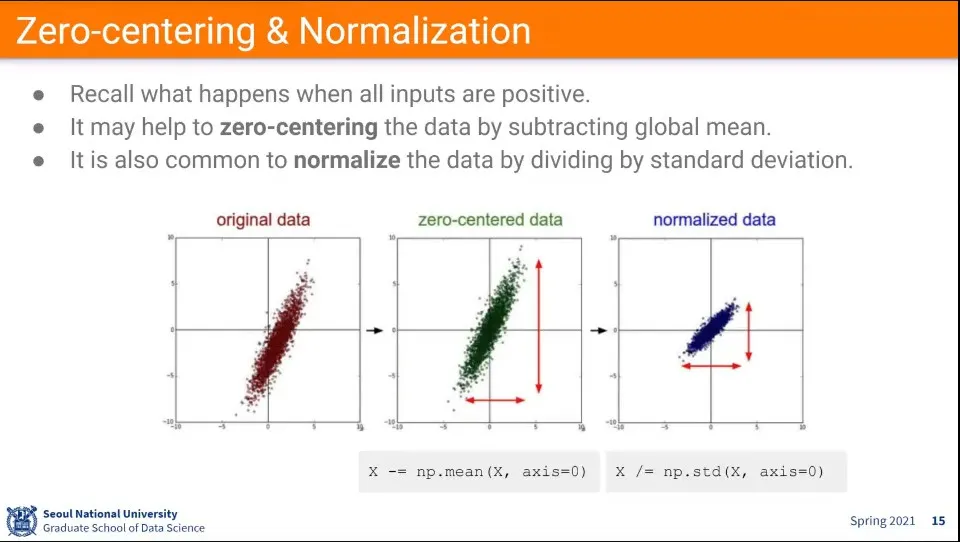
데이터 전처리 단계에서 zero-centering과 normalization을 해준다.
◦
zero-centered는 값이 0을 중심으로 오도록 하는 것 —평균을 뺀다
◦
nomalization은 각 변수들의 크기를 동일하게 하는 것 —표준편차로 나눈다.
▪
어떤 파라미터는 0-1사이의 값을 갖고, 어떤 파라미터는 0-100의 값을 갖는다면 둘다 0-1의 값이 되도록 하는 것
•
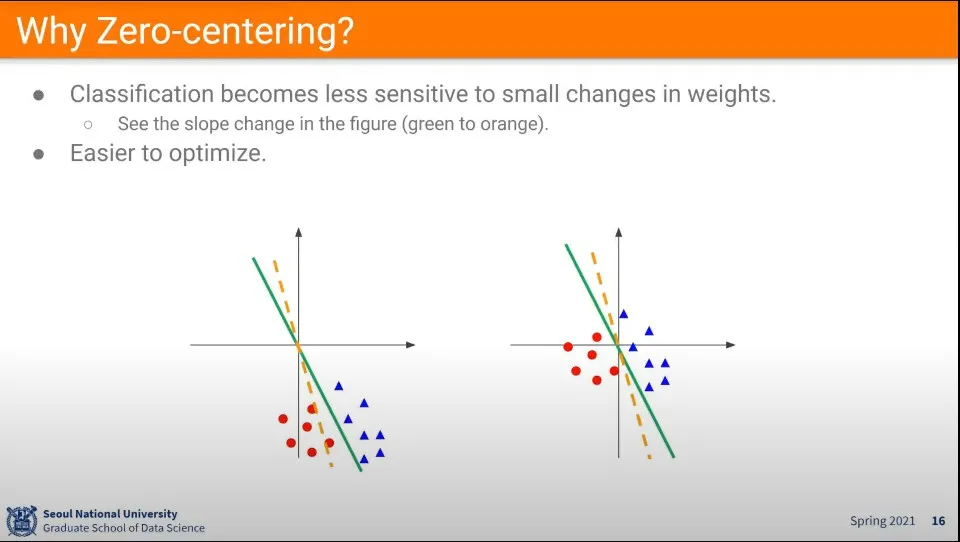
zero-centered를 안 하면 값이 조금만 바뀌어도 기울기가 크게 변해서 fitting이 쉽지 않음. 따라서 zero-centered를 하는게 좋다.
•
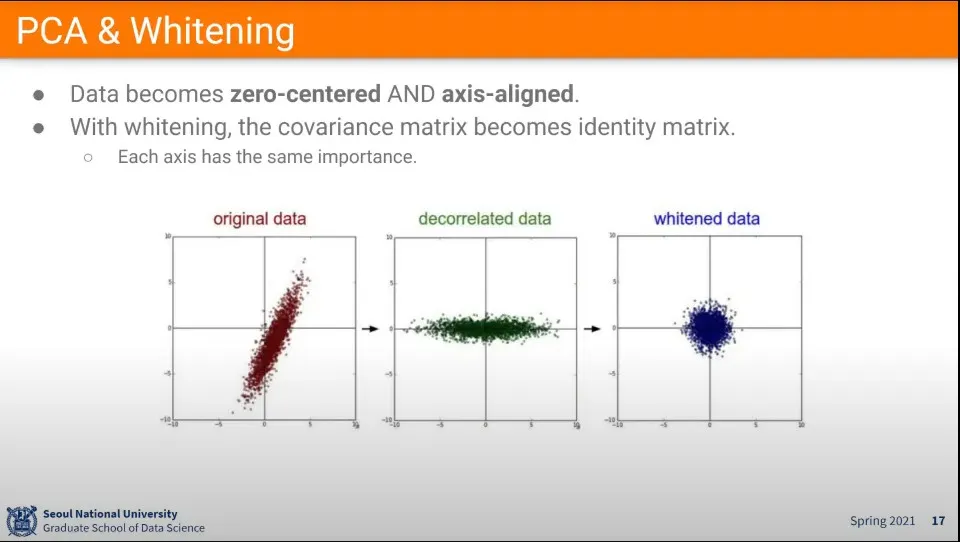
PCA는 zero-centering과 axis-aligned까지 하는 방법
•
whitening은 그렇게 정렬된 데이터를 normalize해주는 것
•
PCA 절차는 위와 같다.
1.
각 값들에 대해 평균을 뺀다 —zero-centered를 한다.
2.
covariance matrix(공분산 행렬)를 계산한다.
•
공분산이란 2개 변수가 함께 변하는 정도를 측정하는 척도이다. 그것을 행렬로 나타낸게 covariance matrix
3.
covariance matrix를 이용해서 eigenvalue decomposition(고유값 분해)을 한다.
•
고윳값 분해란 고유값과 고유벡터로부터 유도되는 고유값 행렬과 고유벡터 행렬에 의해 분해될 수 있는 행렬의 표현이다.
•
그런데 이미지처리에서는 잘 안쓰임. pixcel 단위에서는 안 쓰이고, feature 단위에서는 좀 쓰임
4.
데이터가 가장 많이 보존 되는 순서로 차원을 축소한다.
•
데이터에서 가장 의미가 잘 보존되는거만 남기고 나머지는 없앤다는 의미.
◦
그래서 PCA다. 주성분 분석
◦
이거는 선형대수학을 이해해야 됨
•
데이터 Preprocessing의 예
•
PCA는 유튜브에서 사용함
◦
PCA는 pixcel 레벨에서는 사용 안하고, feature 레벨에서 사용 함
•
가지고 있는 이미지에 다양한 변화를 주어서 데이터셋을 풍부하게 만들어주는 것
•
flip은 Data Augmentation의 기본
◦
horizontal filp은 공짜로 쓸 수 있는데, vertical flip은 경우에 따라 좋을 수도 있고 안 좋을 수 있음. 중력 영향이 있는 경우에는 vertical flip이 어색하다.
•
사진에서 일부분만 랜덤으로 crop
•
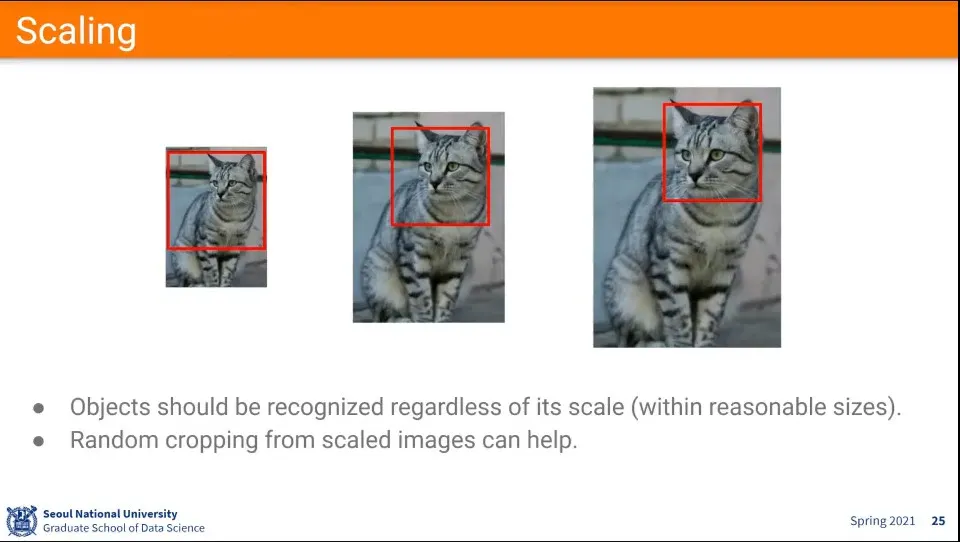
scaling
•
예시
◦
학습할 때
1.
일단 256-480 사이의 값을 랜덤으로 뽑아서 L로 둔다.
2.
주어진 이미지의 짧은쪽이 L이 되도록 scaling 한다.
3.
그 후에 그 안에서 224x224를 뽑는다.
◦
테스트할 때
1.
5개의 scale로 조절하고
2.
224x224를 10개를 뽑고
3.
그 결과를 보고 평균이나 max를 구해서 고양이인지 아닌지 판단한다.
•
이미지를 224x224를 쓰는 이유는 ImageNet 데이터가 그렇게 맞춰져 있어서 AlexNet을 포함하여 초창기 모델들이 이 사이즈에 맞춰져 학습 되어있기 때문에 관례적으로 사용한다.
•
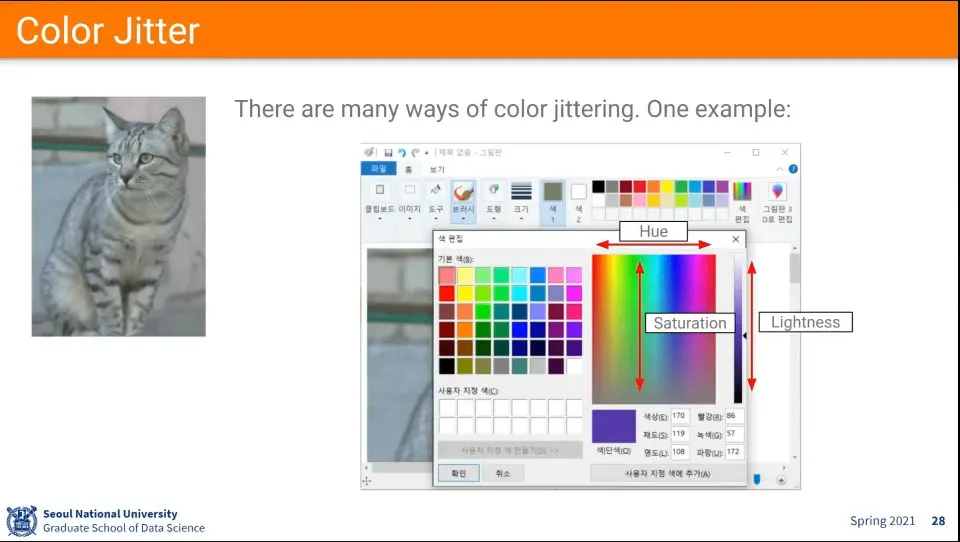
색상을 바꿔주면 조명이 바뀐 것과 비슷한 효과를 낼 수 있다.
•
색상 바꿔주는 것은 HSV를 이용한다.
•
RGB와 HSV의 변환 공식
•
위의 것들 외의 다양한 Augmentation 방법들이 있다.
•
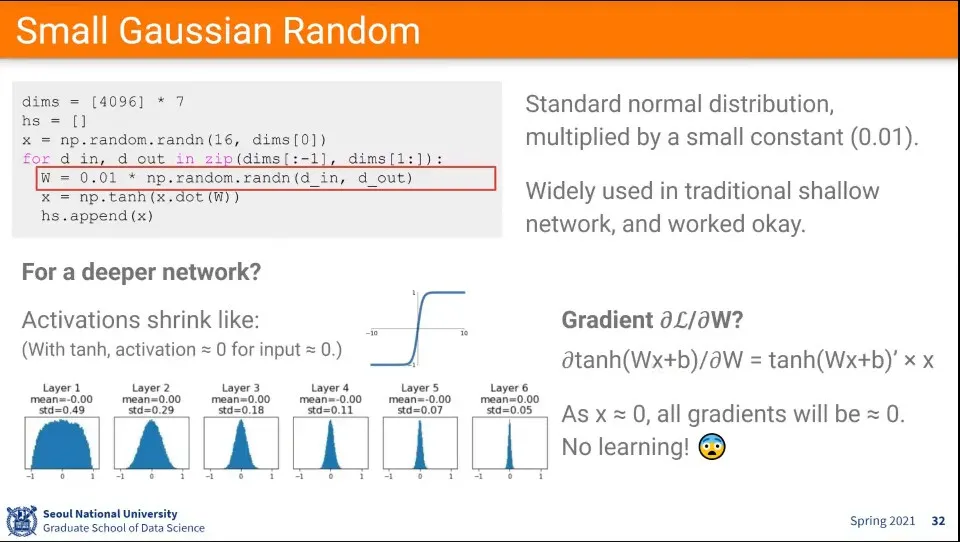
가중치를 초기화할 때 너무 작은 값을 이용했더니 layer를 지날 수록 점점 0에 수렴하는 현상이 발생한다.
◦
이유는 tanh를 로 편미분하면 의 모양이 되는데, 가 에 가까워지면 결과가 에 수렴하게 된다.
◦
다시 말해 작은 input이 들어가게 되면 다 이 된다.
•
가중치를 초기화할 때 너무 큰 값을 이용했더니 layer를 지날수록 지점에 수렴하는 현상이 발생한다.
◦
이유는 마찬가지로 tanh를 로 편미분하면 의 모양이 되는데, tanh에서 가 양의 방향으로 크면 , 음의 방향으로 크면 에 수렴하게 되고, 이 경우 의 앞부분을 으로 만들기 때문에 결과가 0에 수렴하게 된다.
◦
다시 말해 너무 큰 input이 들어가게 되면 에 수렴하는 모양이 나오게 된다.
•
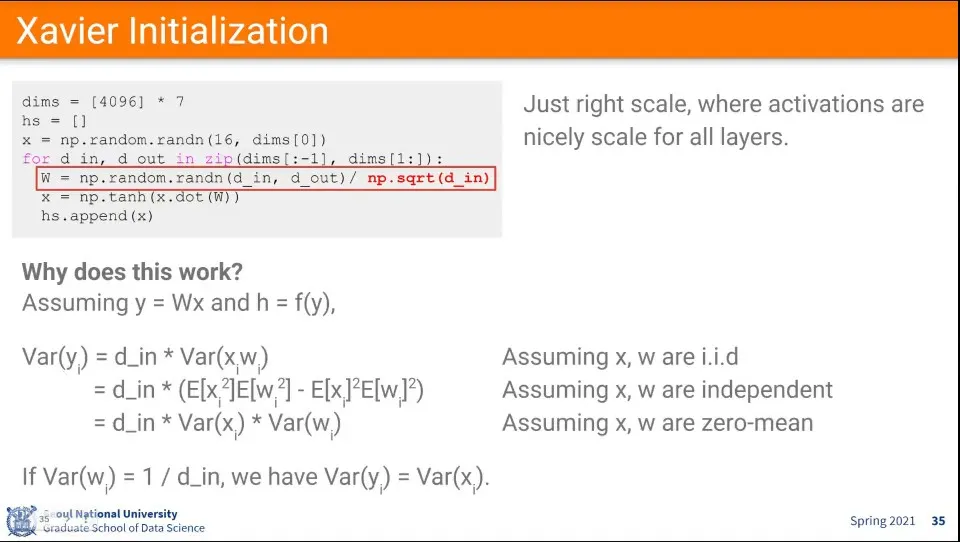
이를 해결하기 위한 대안으로 위와 같은 초기화 수식이 제안된다. - Xavier Initialization
◦
random 값을 input의 개수를 루트 씌운 값으로 나누어서 사용함.
•
x, w가 i.i.d라는 가정하에 위와 같이 전개할 수 있음
◦
(좀 더 상세한 내용은 이 문서 전에 정리한 문서 참조할 것. 슬라이드 자체가 좀 더 상세하게 나옴)
•
ReLU도 초기화 문제가 있음
•
ReLU 초기화는 Kaiming/MSRA 초기화를 사용함