•
이전에 들었던 유사한 부분이 많기 때문에 간략히 정리. 상세 내용은 아래 페이지 참조
•
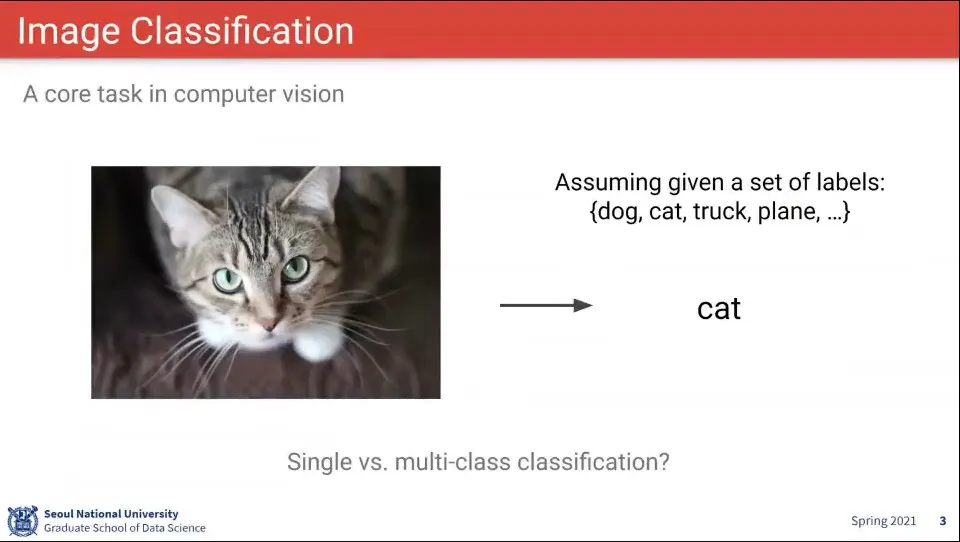
이미지 분류 문제는 이렇게 정의할 수 있다.
◦
정의된 Label 셋이 있고 사진을 보고 Label을 맞추는 것
•
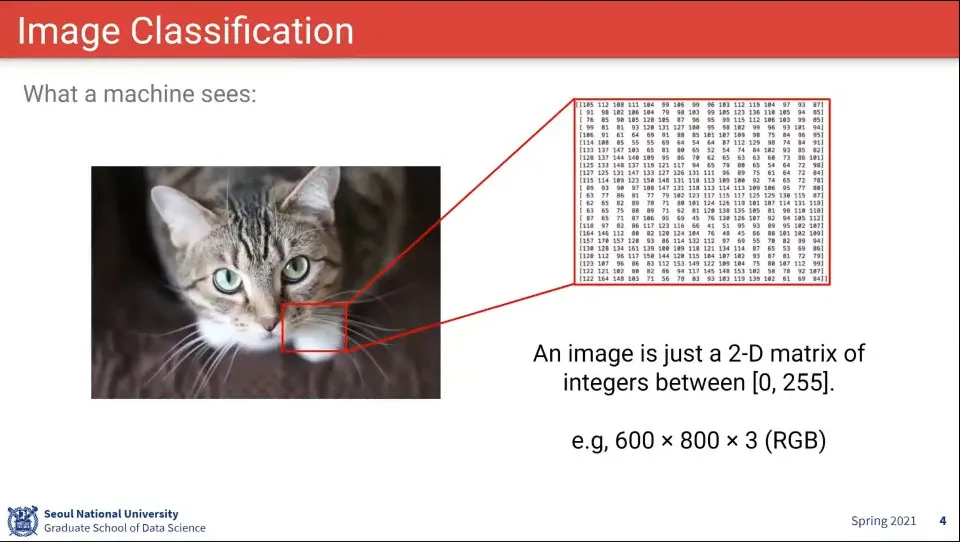
이미지는 숫자로 되어 있음
•
이미지 인식에서 어려운 부분. 동일한 물체지만 아래와 같은 차이가 있을 수 있음
◦
크기가 다르거나
◦
각도가 다르거나
◦
배경에 묻히거나
◦
조명이 달라지거나
◦
일부가 가려지거나
◦
형태가 바뀌거나
◦
동일한 분류 내에 또 다른 분류가 있음
•
이미지 분류는 위와 같이 접근할 수 있다. 이미지를 받아서 해당하는 라벨을 output으로 내보냄
•
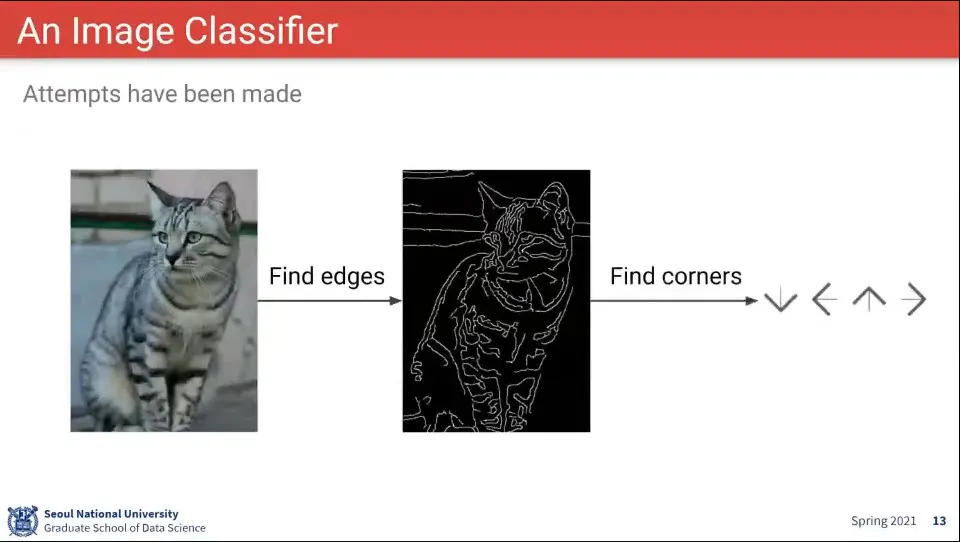
이런 식의 접근으로는 대상을 분류하기가 어렵다.
•
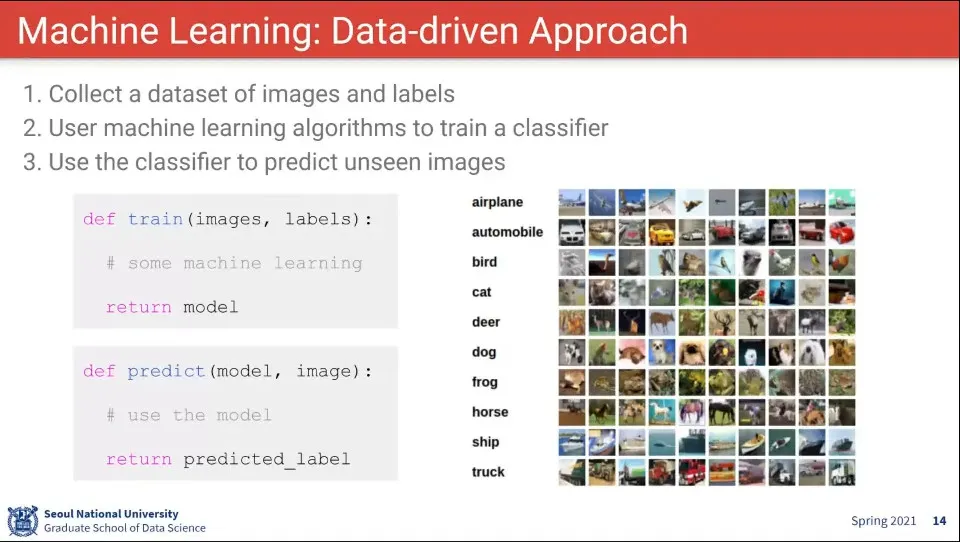
머신러닝은 데이터 기반 접근 방법
◦
학습 과정과 예측 과정을 분리
•
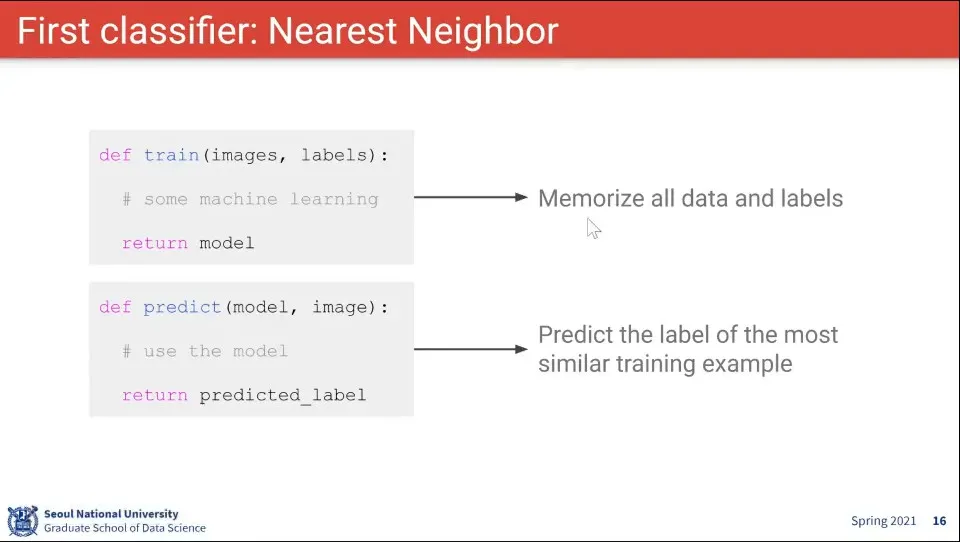
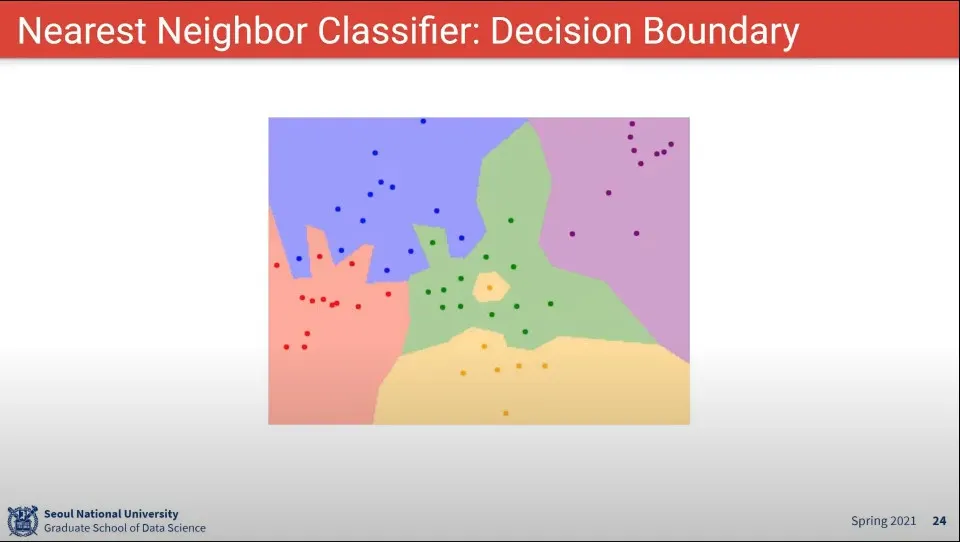
Nearest Neighbor Classifier는 데이터를 그냥 저장해 두고 있다가, 이미지가 입력 되면 저장된 데이터에서 가장 가까운 것을 찾는 것
•
입력 이미지와 가장 가까운 것을 어떻게 찾을까?
•
이런 식의 유사도 계산 함수가 필요할 것 같다. 그런데 이건 어떻게 할 수 있을까?
•
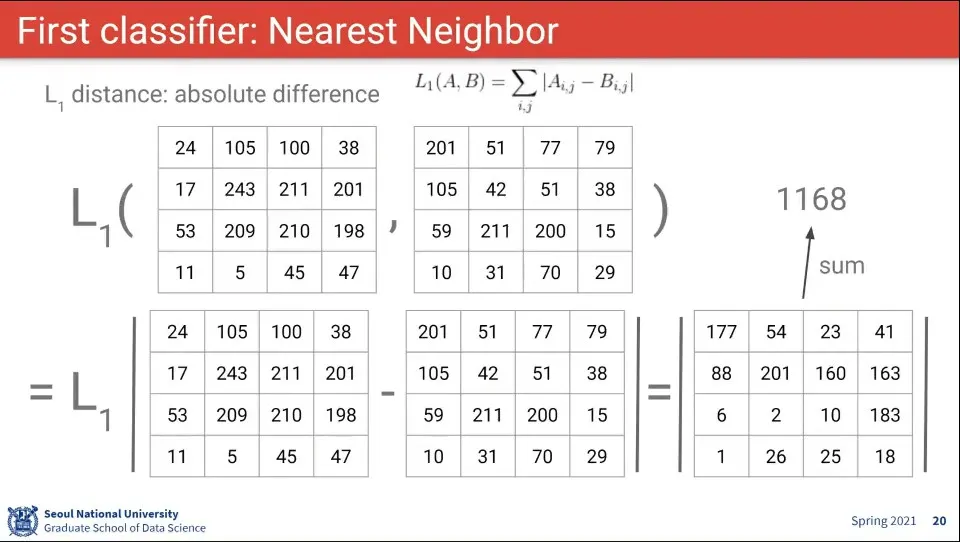
데이터가 픽셀 정보로 들어오므로 이미지 간의 픽셀 차이를 계산해 보자
•
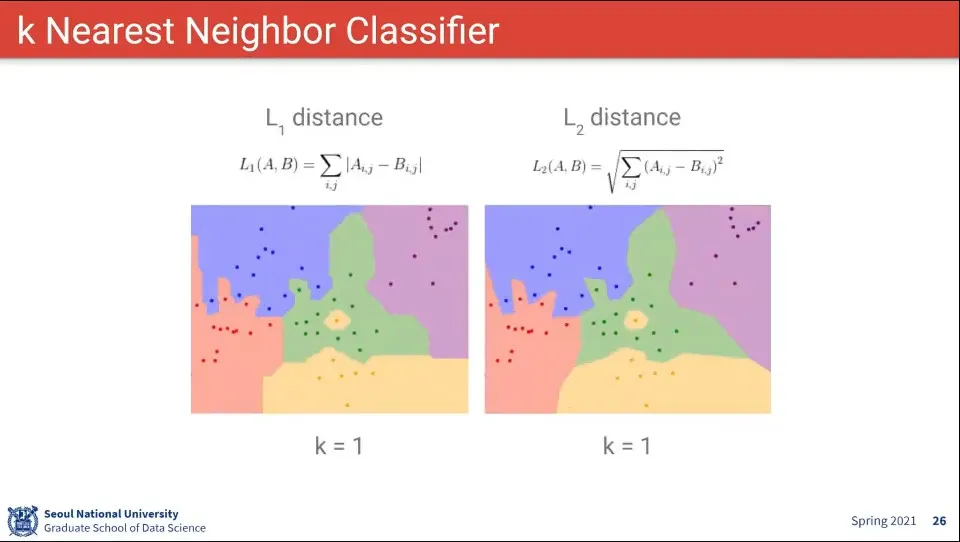
L1 거리를 적용하면 위와 같다. 차이의 절대값의 합
•
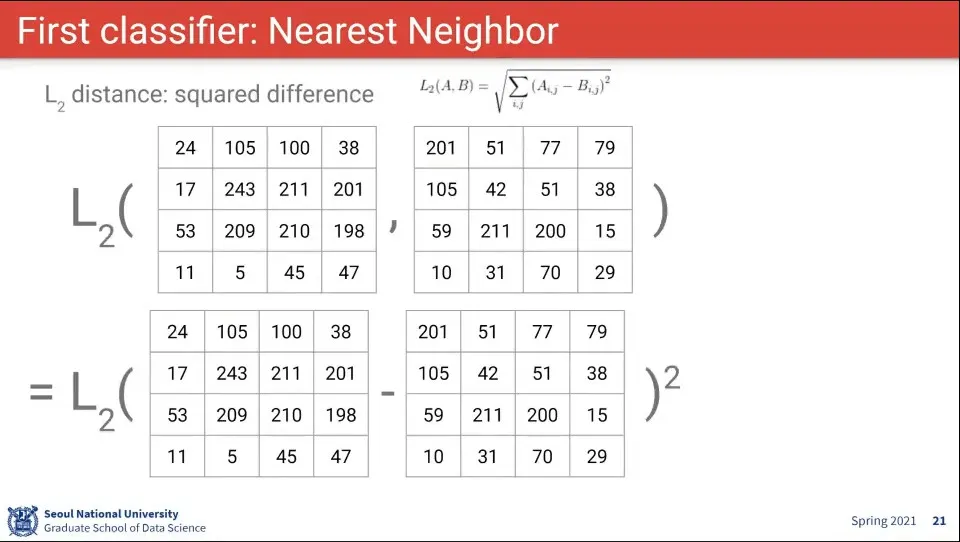
L2 거리를 적용하면 위와 같다. 차이의 제곱의 합
•
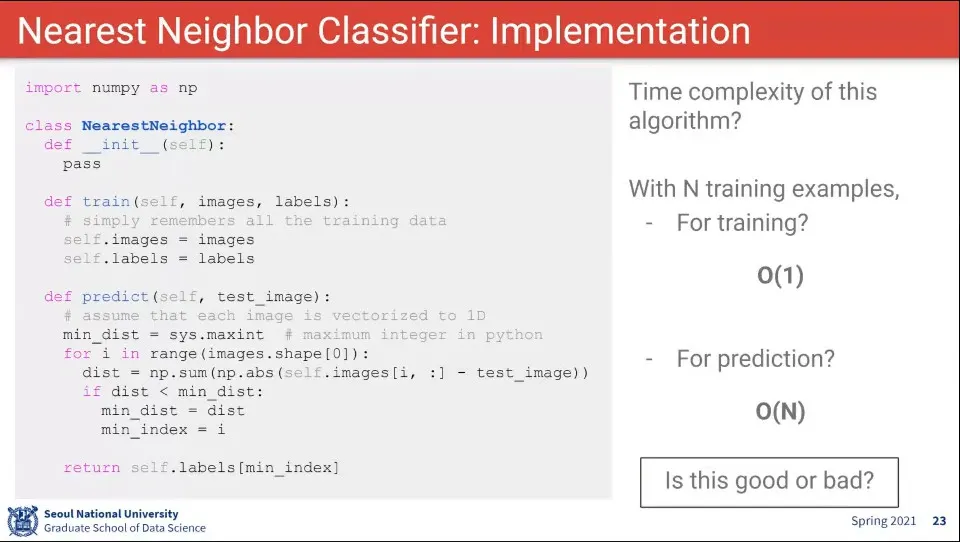
코드를 짜보면 위와 같이 할 수 있다.
•
그런데 이렇게 짜면 예측 시간이 너무 오래 걸리기 때문에 좋지 않다.
•
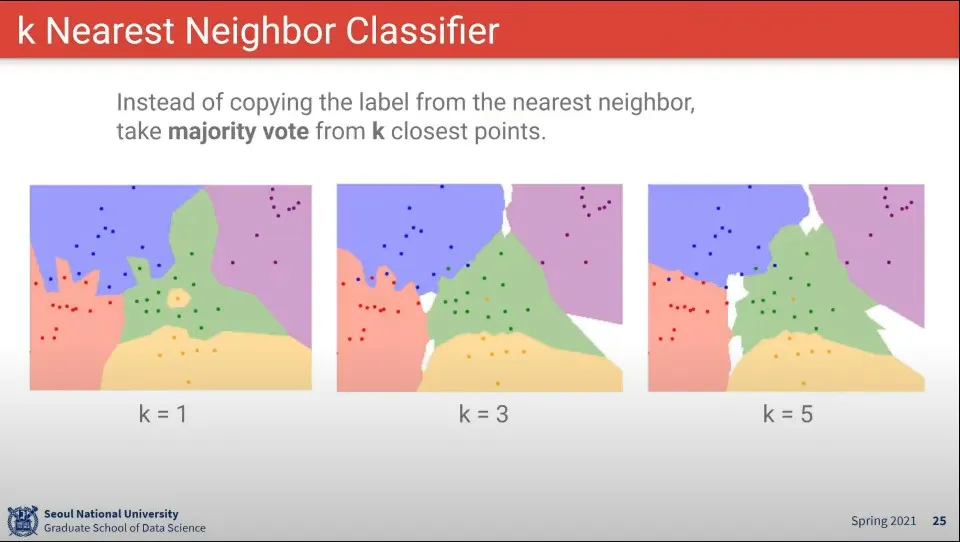
Nearest Neighbor 의 결과 예시
◦
K는 가장 가까운 것을 K개 이상을 사용한 결과 —일종의 투표 같은 셈
•
L1을 쓰나 L2를 쓰나 큰 차이는 없다.
•
K를 몇 개로 할 것이냐, 거리를 얼마로 할 것이냐를 정하는 것이 애매함
•
Nearest Neighbor로는 위와 같은 문제가 있음. 사람이 보기에는 같지만, 픽셀 정보면 조금 다르게 한 것을 구분하지 못 함
•
또한 차원의 저주 문제도 갖고 있음
◦
차원이 늘어날 수록 필요로 하는 데이터의 숫자가 exponential 하게 커짐
•
위와 같은 이유로 Nearest Neighbor는 잘 안 쓰지만, 쓰게 된다면 위와 같은 방법을 적용해서 해볼 수 있다.
◦
데이터 노말라이징
◦
차원 리덕션
◦
학습/검증 셋 분리
◦
모든 점에 대해 검사하지 않고 적당하게 가까운 점들을 갖고 판단
•
이미지를 받으면 어떤 Label을 뱉어주는 어떤 함수를 생각해 볼 수 있다.
•
이미지에 어떤 parameter를 적용해서 label을 뽑아주는 것을 생각해 볼 수 있다.
•
input에 대해 학습된 Weight를 적용해 주면 어떤 label을 의미하는건지를 output으로 줌
•
함수는 input x와 학습된 Weight 를 선형으로 결합해서 Label을 출력해주는 모델을 생각할 수 있다.
•
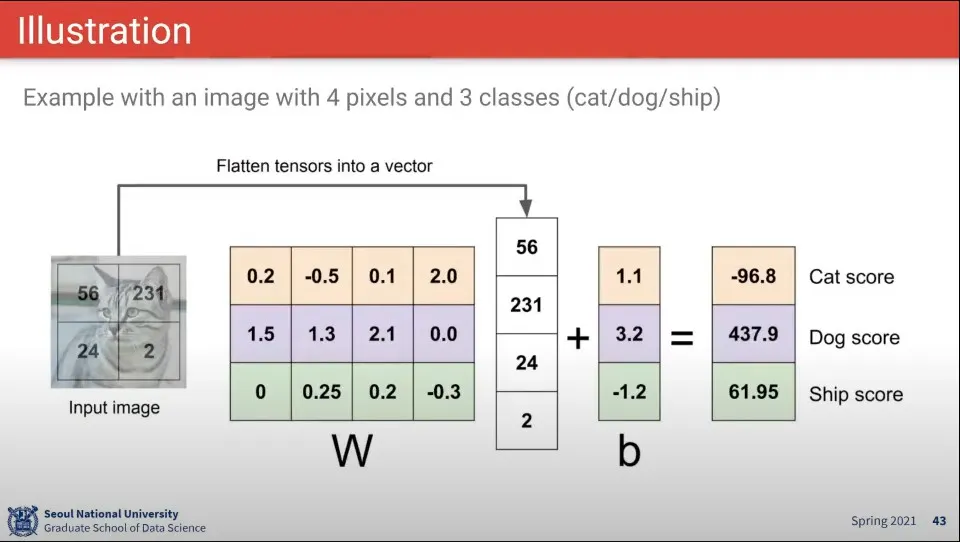
위와 같은 예에서 이미지 x와 파라미터 W, 편향 b의 크기는 위와 같이 생각할 수 있다.
•
bias를 따로 더해주는 것은 번거로우므로 아예 input과 w의 행렬 안에 포함 시켜서 계산한다.
◦
input에 1행, w에 1열을 추가해 줌
•
함수를 이렇게 정의하면 W만 저장해 두면 되기 때문에 공간이 절약되고, 계산 속도도 빠르다.
•
계산 예
•
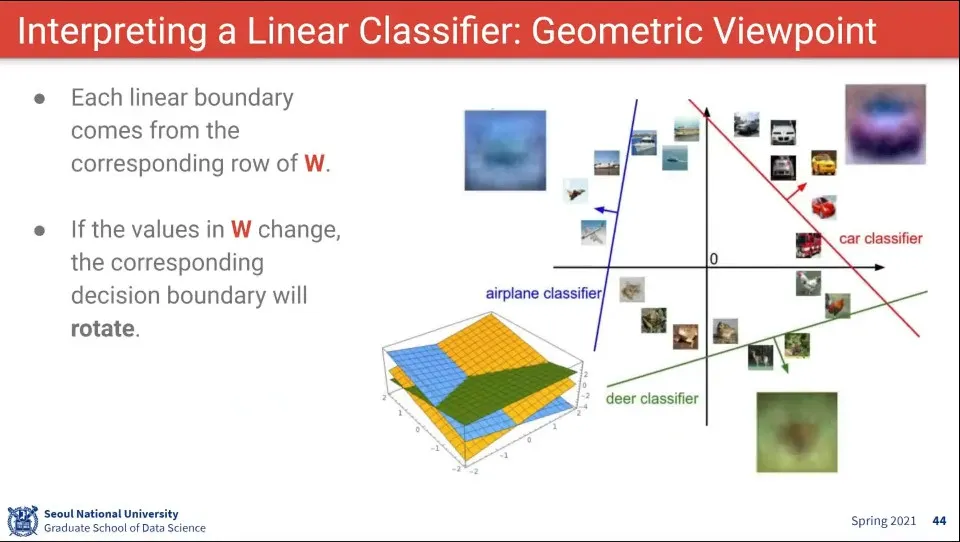
위 함수를 시각해 보면 위와 같다. 각 선형으로 그어진 선 혹은 면을 기준으로 그 영역에 해당하는 label을 고르는 것
•
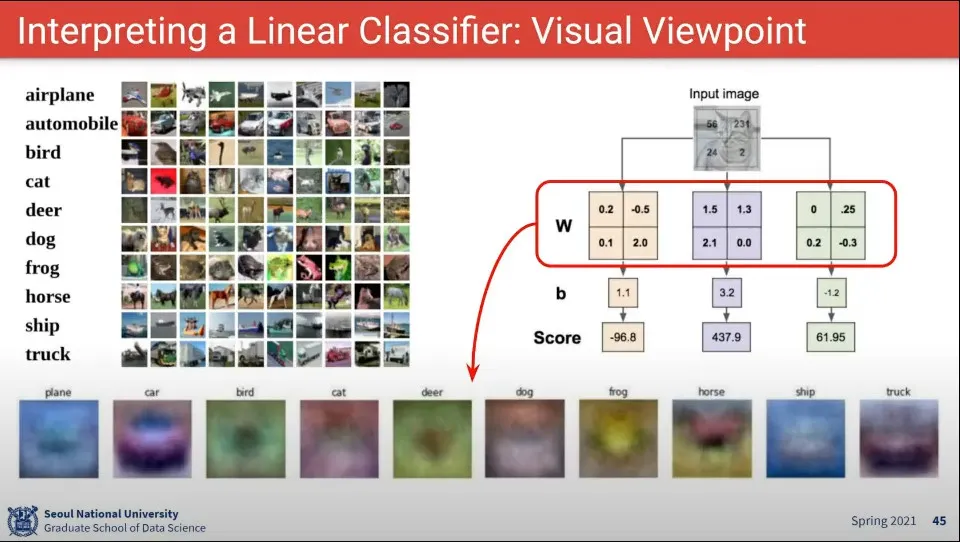
학습한 W를 다시 그려보면 아래와 같이 보인다.
◦
차나 말은 실제로 차나 말처럼 보이고, 전혀 알아보기 어려운 것도 있다.