•
이전에 들었던 유사한 부분이 많기 때문에 간략히 정리. 상세 내용은 아래 페이지 참조
•
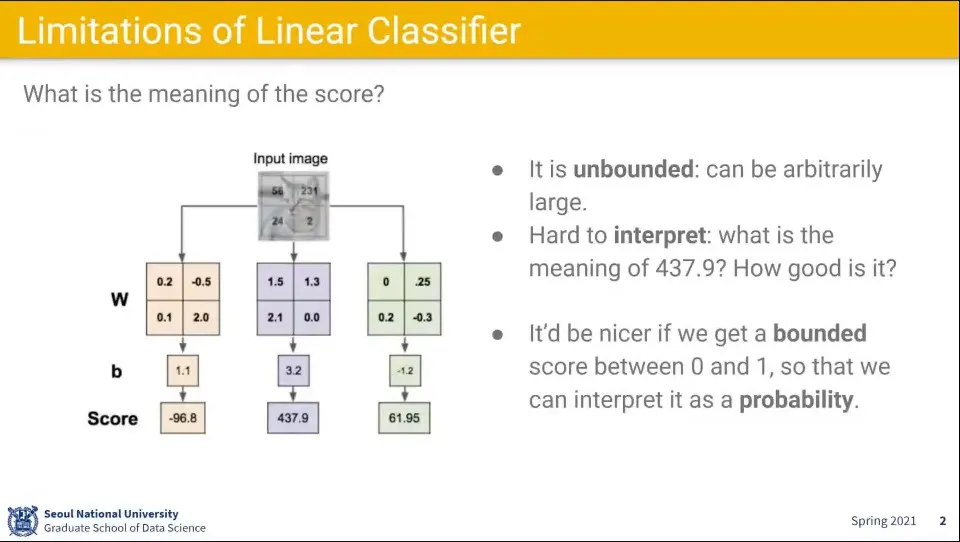
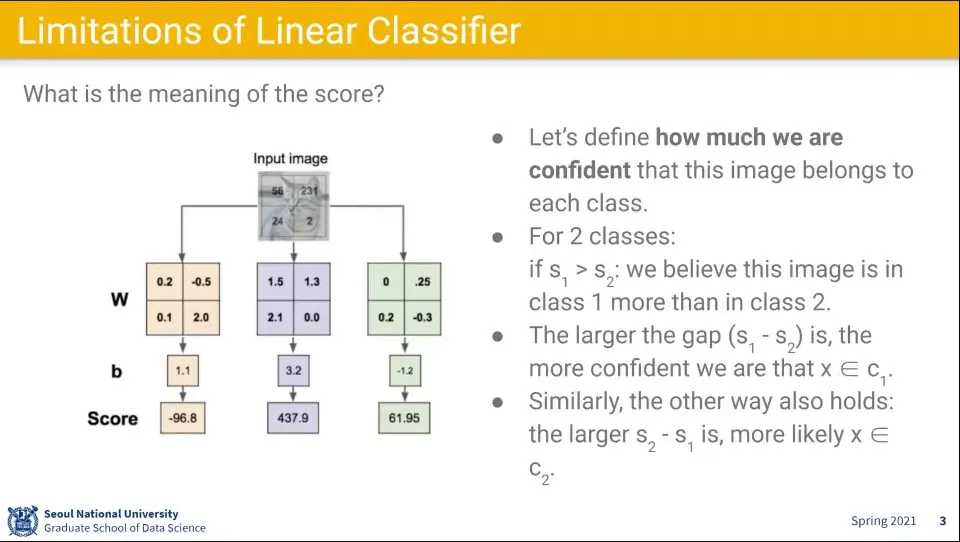
앞서 배웠던 선형 함수에 대해 class 별로 input 이미지를 계산하면 위와 같이 결과가 나오는데, 이 결과는 이해하기 어려운 결과이다.
•
때문에 이것을 사람이 이해하기 쉽게 결과를 확률로 표현할 수 있다.
•
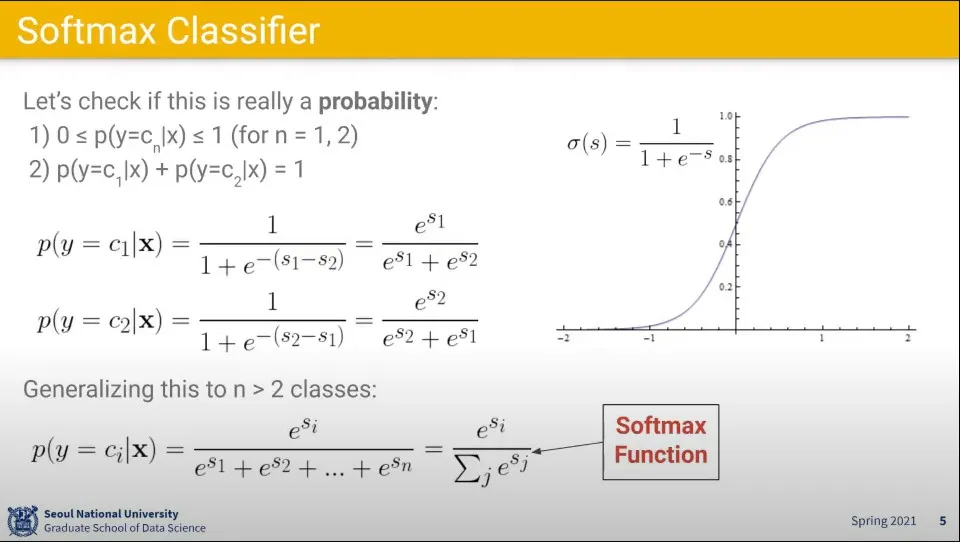
이럴 때는 sigmoid 함수를 사용할 수 있다.
•
그런데 결과는 클래스별로 나타나므로, 위의 sigmoid 함수를 전체에 대해 확률로 표현할 수 있게 softmax 함수를 씌운다.
•
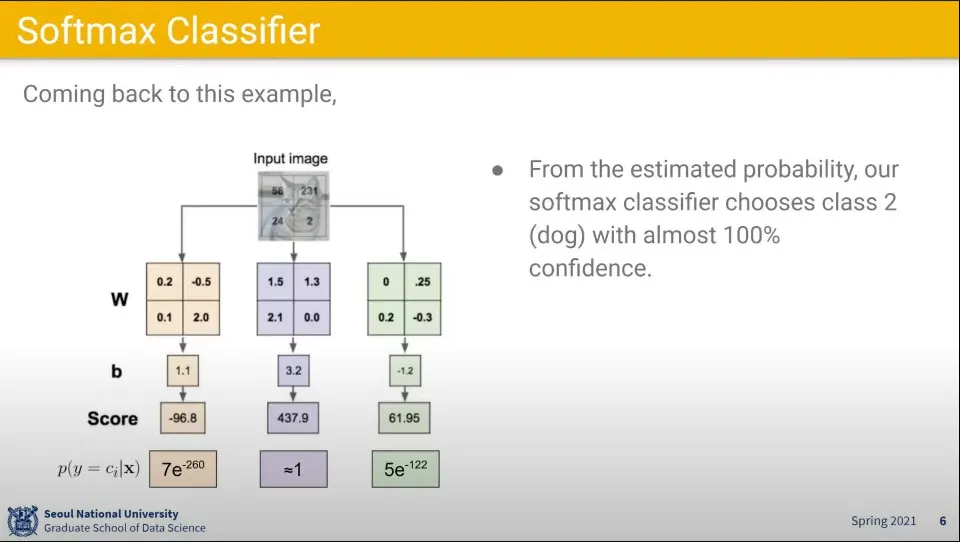
앞선 결과에 대해 softmax를 씌우면 결과를 확률로 이해할 수 있다.
◦
위 예에서는 가운데일 확률 1에 가깝고 나머지 2개는 거의 0에 가깝다.
•
머신러닝은 데이터 기반 접근이다. 따라서 는 데이터로부터 학습해야 함.
◦
처음에는 를 랜덤으로 초기화하고
◦
입력에 대해 를 곱해 예측 결과 를 구한다.
◦
그 후에 실제 정답 과 예측 결과 의 차이를 바탕으로 예측이 잘 됐는지 판단한다.
◦
그 결과를 바탕으로 를 업데이트 한다.
◦
가 와 같아질 때까지 위 과정을 반복한다.
•
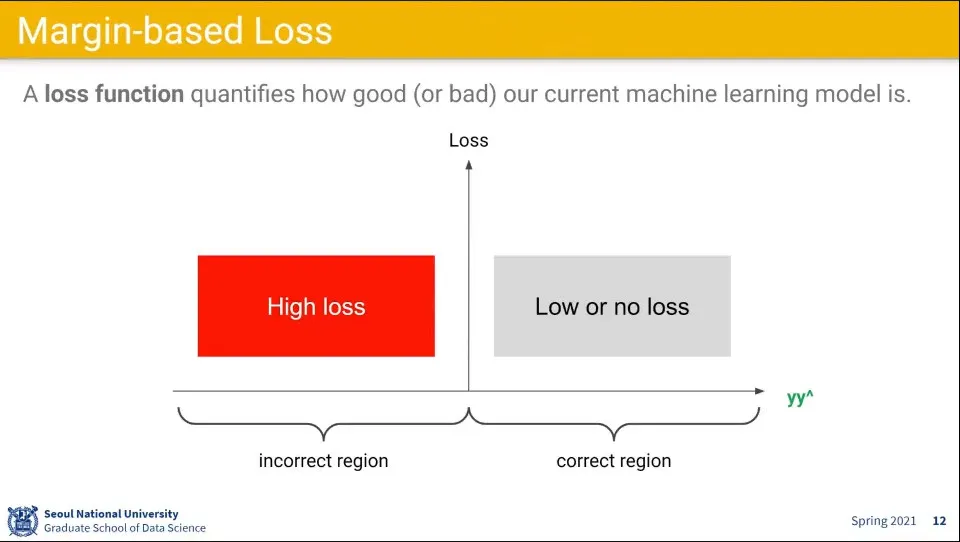
Loss 함수는 예측이 맞았는지 틀렸는지를 계량화 해주는 함수이다.
◦
와 의 차이가 클수록 큰 숫자가 나오고 비슷할 수록 0에 가까운 값이 나오도록 디자인 해 볼 수 있다.
•
위와 같은 조건에 대해 Discriminative 세팅을 할 수 있다.
◦
에 대해 +1, -1의 정답을 설정하고, 또한 +1, -1이 나오도록 함
◦
이렇게 되면 가 +1이었는데 이 +1이거나, 가 -1이었는데 이 -1이면 예측이 맞은 것이고, 그 외는 틀린 것이 된다.
◦
이때 예측의 결과를 측정하기 위해 와 을 곱하여 계산한다. 예측이 맞았다면 곱의 결과가 +가 나오고, 틀렸다면 -가 나올 것이다.
•
위와 같은 설정이면 정답이 맞을때 결과가 그래프 오른쪽으로 나오고, 틀렸을 때는 그래프 왼쪽으로 나온다.
◦
따라서 틀렸을 때는 Loss가 크고, 맞았을 때는 Loss가 작게 나오도록 하는 함수를 생각할 수 있다.
•
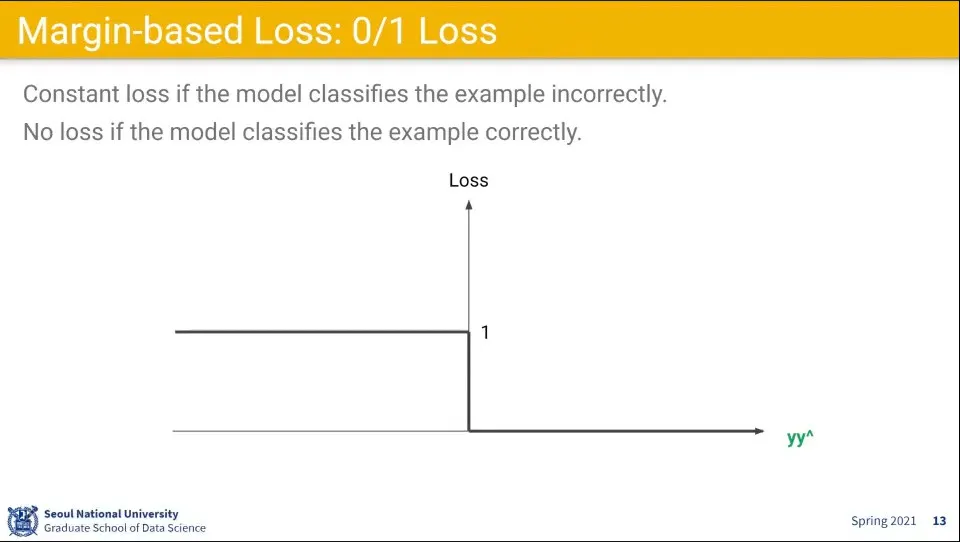
틀렸을 때는 1, 맞았을 때는 0이 나오는 이러한 함수를 0/1 Loss라고 한다.
•
그런데 이 함수는 문제점이 있다.
◦
0인 지점에서 미분이 안 됨
◦
또한 맞췄을 때라도 Loss가 0이면 문제가 될 수 있음
•
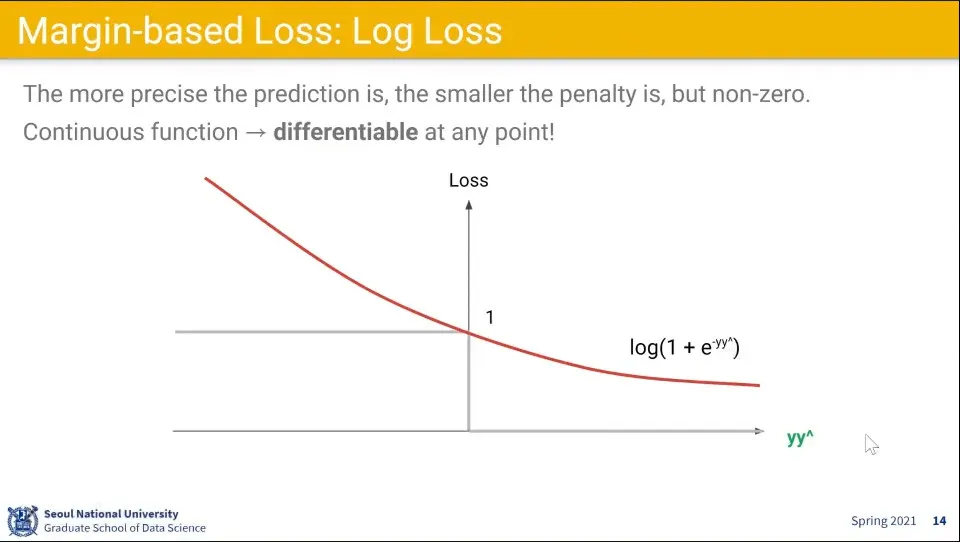
0/1 Loss의 문제를 개선해서 위와 같은 Log 함수 로스를 생각해 볼 수 있다.
•
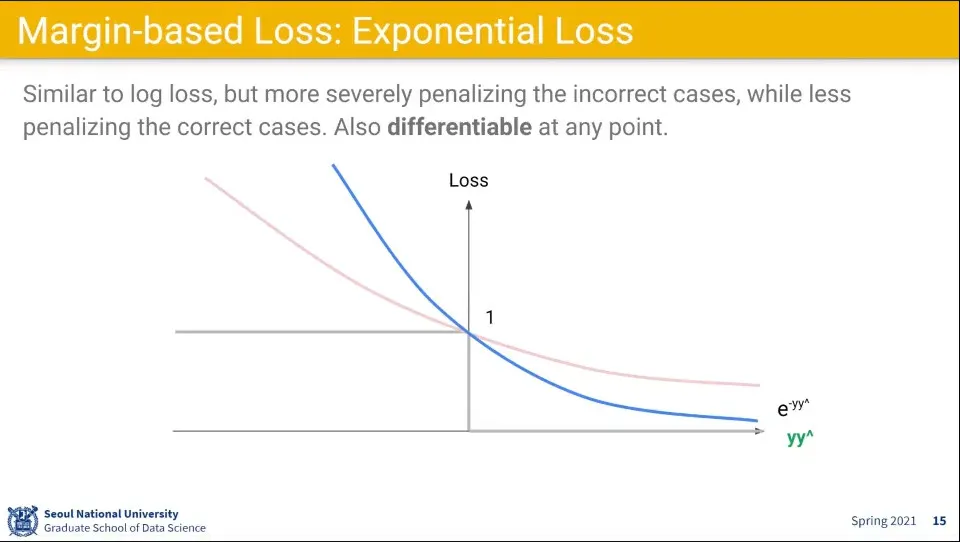
Log Loss보다 더 극단적인거는 Exponential Loss가 있다.
•
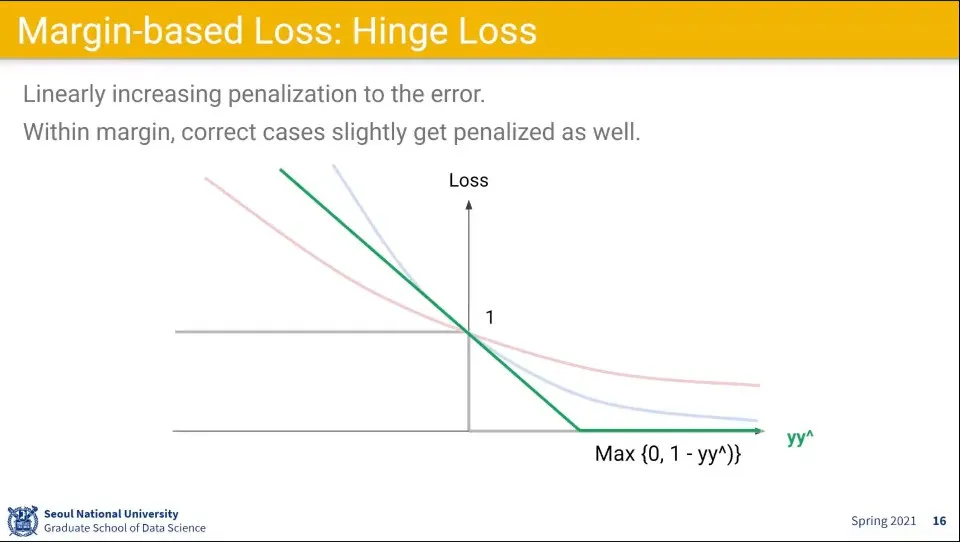
Margin을 둬서 사용하는 Hinge Loss 함수가 있다.
◦
Marin 이내면 맞춰도 Loss를 좀 주고, Margin을 넘으면 0을 준다.
◦
이것은 SVM에서 사용한다.
•
Hinge Loss는 선형 함수라 미분을 하지 않기 때문에 성능이 좋다.
•
Exponential Loss는 값이 극단적이라 잘 안 사용하고 Log Loss와 Hinge Loss는 자주 사용한다.
•
Discriminative와 다르게 Probabilistic 세팅이 있는데, 이 경우에는 가 0과 1의 값을 갖는다.
◦
이때 은 0과 1사이의 확률 값이 나오도록 함.
•
여기서 사용하는 Loss 함수로 Cross Entopy를 사용한다.
•
Cross Entropy 함수는 위 이미지의 파란색 화살표의 0-1 구간의 모양이 나오기 때문에 많이 사용한다.
•
KL Divergence라는 함수도 사용하는데, 이것은 엄밀히 거리 계산하는 것은 아님. 참고용
◦
KL Divergence는 실용적으로는 많이 쓰임
◦
그러나 삼각형에서 두 변의 합이 나머지 한 변의 합보다 크다는 조건이 성립을 안 함
•
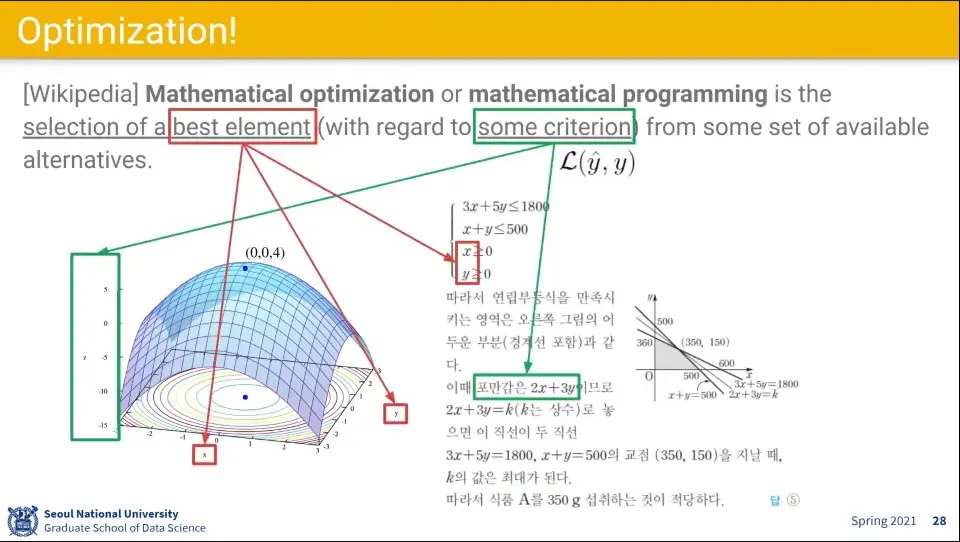
최적화는 주어진 조건을 최적화하는 x, y 조합을 찾는 문제와 같음
•
최적화를 위한 몇 가지 아이디어
•
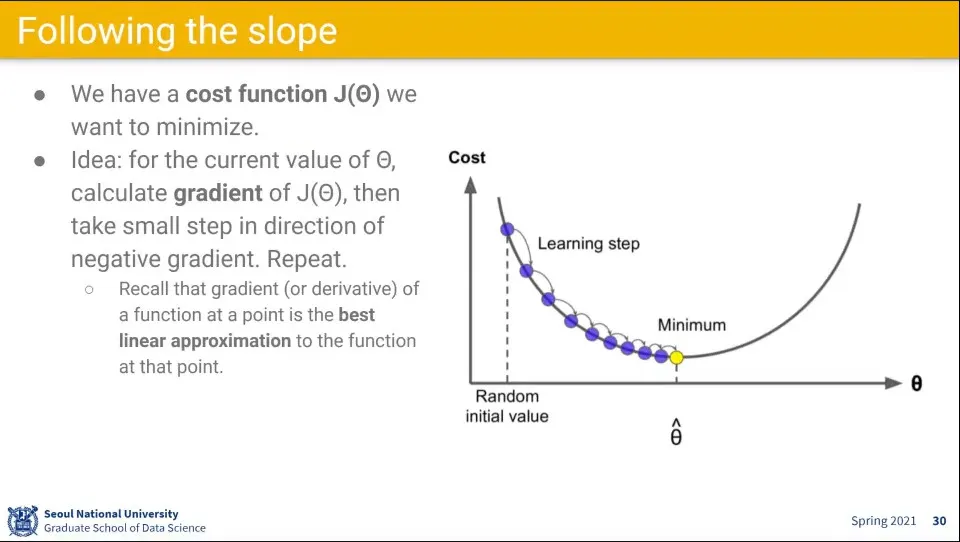
최적화를 위해 cost 함수의 gradient를 계산하고 파라미터를 업데이트 해주는 것을 반복한다.
•
식은 위와 같이 생각할 수 있음
◦
업데이트 하면서 파라미터를 줄여야 하기 때문에 기존 값에 대해 learning rate를 곱해서 새로운 파라미터를 구한다.
•
Gradient Descent 방법에도 한계가 있다.
◦
지역 최적점에 빠질 수 있음
◦
지역 최적점이면서 동시에 지역 최고점인 saddle point에서는 움직일 수 없음
◦
미분 불가능한 지점이 있음 - 미분이 안되면 내려갈 수가 없다.
◦
계산이 오래 걸림
•
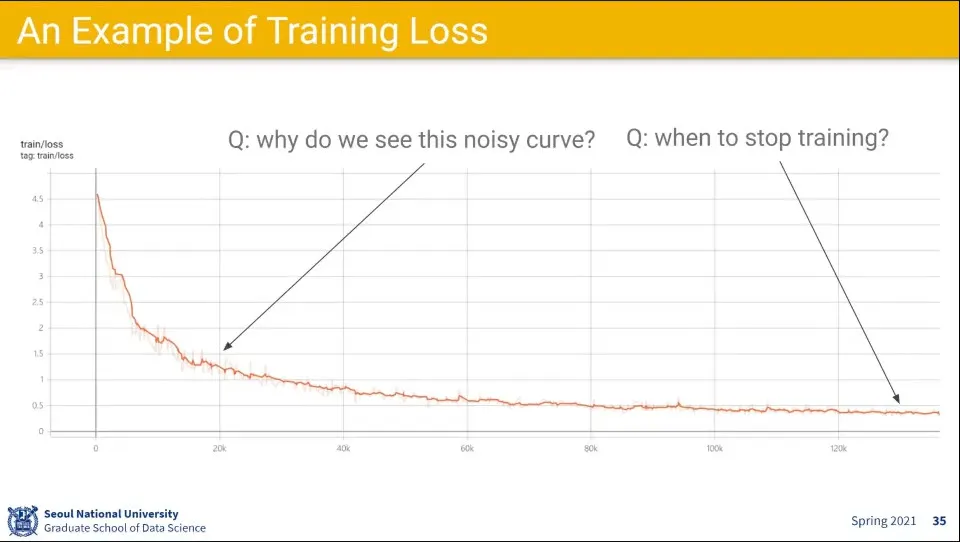
Gradient Descent의 계산이 오래 걸리는 부분을 개선한 것이 Stochastic Gradient Descent(SGD)이다.
◦
전체 데이터에 대해 계산을 다 하지 않고, mini-batch 사이즈만 가지고 계산해서 진행 함.
◦
어차피 모든 데이터도 현실에 대해 부분 데이터이기 때문에 그걸 써도 그게 확실하다는 보장은 할 수 없다. 따라서 일부 데이터만 뽑아서 처리한다.
◦
batch size도 일정 수준 올라가면 2배가 늘어도 성능이 그만큼 올라가지 않기 때문에 적절한 수준을 찾는게 좋다.
•
SGD 예
•
우리의 목표는 데이터로부터 일반화된 패턴을 학습해서 새로운 데이터에 대해서도 예측을 잘 수행하는 것
•
그런데 학습 데이터에 대해서만 집중하면 overfitting이 발생할 수 있다.
•
그것을 방지 하기 위해 test data 혹은 eval data라고 불리는 데이터셋을 사용한다.
◦
test data는 오로지 테스트에서 사용해야 하고, 학습 과정에서는 절대 사용되어서는 안 된다. —학습할 때 매번 랜덤으로 데이터를 나누면 테스트 데이터가 학습 과정 중에 들어갈 수 있으므로 안 됨. 아예 별도로 데이터를 따로 빼 놔야 함
•
테스트 셋은 일반적으로 전체 데이터의 10-20% 정도만 따로 빼서 사용한다.
•
모델을 만들기 위해 다양한 하이퍼 파라미터 셋을 설정해야 한다. 그런데 이 파라미터 셋이 학습 과정에서 선택하게 되는데 테스트에서 제대로 동작이 안 될 수 있다. 이것을 위해 validation set이라는 것을 또 설정한다.
•
학습 데이터셋과 검증 데이터셋, 시험 데이터셋은 위와 같이 설정해서 할 수 있다.
1.
최초 70% 정도의 training set만 가지고 학습
2.
그후 20% 정도의 validation set만 가지고 검증
3.
1-2를 반복하면서 파라미터를 최적화
4.
그 다음으로 training + validation set을 합해서 학습
5.
마지막으로 eval set으로 시험
•
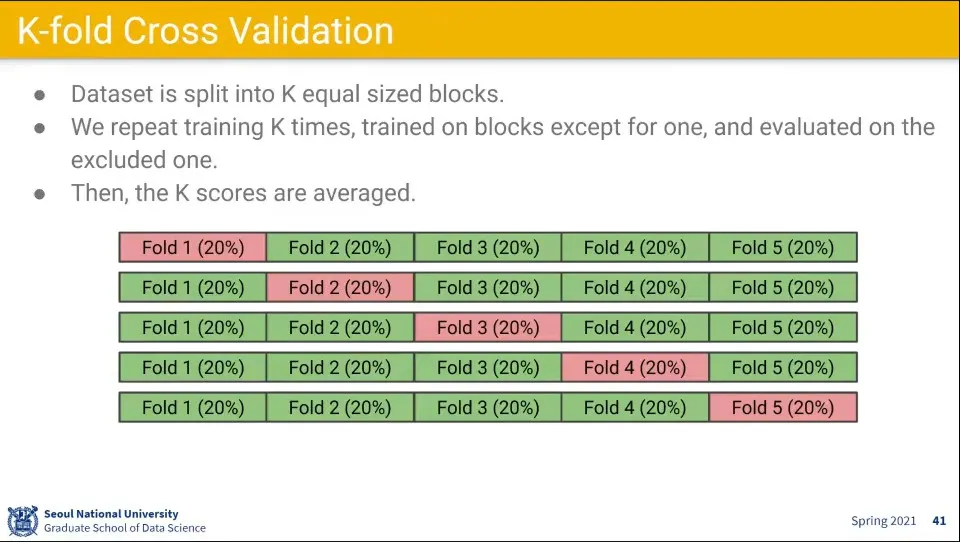
위 과정이 번거롭기 때문에 K-fold Cross Validation 방법을 사용할 수 있는데, 많이 쓰이지는 않음
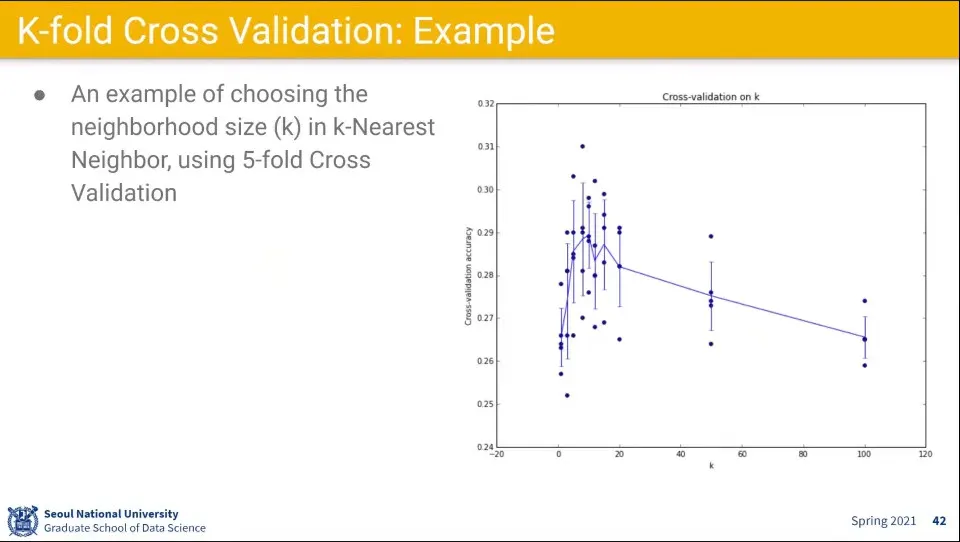
•
K-fold Cross Validation 적용 예