DINO(DIstillation with NO label)
DINO는 BYOL과 유사한 self-supervised 모델로 특정 task를 직접 해결하기 보다는 representation을 학습하여 downstream task에 전이시키는 목적의 pretext task를 수행하는 모델이다. BYOL이 강화학습에서 착안하여 online, target 네트워크를 사용한 것과 달리 DINO는 student-teacher network의 distillation 방식을 사용한다.
DINO 자체는 ViT에 한정된 모델이 아니지만, 논문의 저자들은 ViT를 사용할 때 CNN 기반 모델(ResNet)에 비해 훨씬 나은 성능을 얻을 수 있었다고 주장한다. 심지어 계산 효율성도 CNN에 비해 ViT가 더 좋았다고 함.
이것은 ViT가 특정 vision task에 대해 대규모 데이터셋에서 CNN과 동등한 수준을 얻기는 했었지만, representation 학습에서는 CNN을 능가하는 능력을 가질 수 있다는 것으로 보인다. representation 학습에서는 아무래도 대규모 데이터셋이 필요한데, Transformer가 데이터셋의 Scaling에 따라 성능이 좋아지는 것으로 유명하기 때문에 그럴 것으로 생각 됨.
Distillation
DINO는 distillation 방식을 따라 student, teacher 네트워크를 구성하여 student가 teacher의 출력을 예측하도록 한다. 다만 DINO에서는 student와 teacher에게 동일한 이미지의 서로 다르게 augmented된 입력을 제공한 후 student와 teacher의 결과에 대한 loss를 계산해서 student의 파라미터를 업데이트하는 방식을 사용한다. 이것은 기존의 distillation 방식에 self-supervised를 적용한 형태이다.
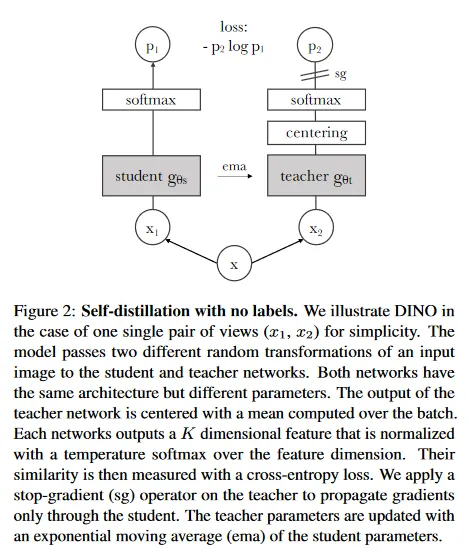
보다 정확히 서로 다르게 augmented된 이미지를 student와 teacher 네트워크에 각각 입력한 다음, student의 결과에 대해 softmax만 씌우고, teacher의 결과에 대해서는 배치 내 출력의 평균을 중심으로 조정하는 centering 과정을 거친 후에 softmax를 씌운다. 최종적으로 그 두 결과에 대해 loss를 계산한 후 student에 대해서만 역전파를 수행한다. (이미지에서 sg는 stop gradient)
추가로 teacher에 대해 역전파를 수행하지는 않지만 teacher를 고정하는 일반적인 distillation과 달리, student의 파라미터 를 이용하여 teacher의 파라미터 를 아래와 같이 exponential moving average 형식으로 업데이트하는 방식을 취한다. 이것은 student가 teacher에 더 안정적으로 수렴하도록 한다.
여기서 는 학습하는 동안 에서 로 증가하는 코사인 스케쥴을 따른다.
보다 상세한 구현 사항이나 수식에 대해서는 참조 자료의 논문 페이지 참조.
Sample Code
DINO의 학습 방법에 대한 pseudo-code. 아래 코드에서 student(gs)와 teacher(gt)에 대한 backbone 모델은 ResNet이나 ViT 등을 자유롭게 사용할 수 있다. 아키텍쳐 샘플 코드는 생략.
코드에서는 동일한 이미지를 2개로 증강시킨 후에 student와 teacher에 모두 입력하고, 2가지 버전을 교차로 loss를 계산하는 형식을 취한다. 이것은 원래의 이미지가 동일했기 때문에 가능하며, 단순히 동일하게 증강된 버전에 대한 loss를 계산하는 것보다 더 일반화가 잘 될 수 있음.
# gs, gt: student and teacher networks
# C: center (K)
# tps, tpt: student and teacher temperatures
# l, m: network and center momentum rates
gt.params = gs.params
for x in loader: # load a minibatch x with n samples
x1, x2 = augment(x), augment(x) # random views
s1, s2 = gs(x1), gs(x2) # student output n-by-K
t1, t2 = gt(x1), gt(x2) # teacher output n-by-K
loss = H(t1, s2)/2 + H(t2, s1)/2
loss.backward() # back-propagate
# student, teacher and center updates
update(gs) # SGD
gt.params = l*gt.params + (1-l)*gs.params
C = m*C + (1-m)*cat([t1, t2]).mean(dim=0)
def H(t, s):
t = t.detach() # stop gradient
s = softmax(s / tps, dim=1)
t = softmax((t - C) / tpt, dim=1) # center + sharpen
return - (t * log(s)).sum(dim=1).mean()
Python
복사