Search
Duplicate

AI/ Triangulation

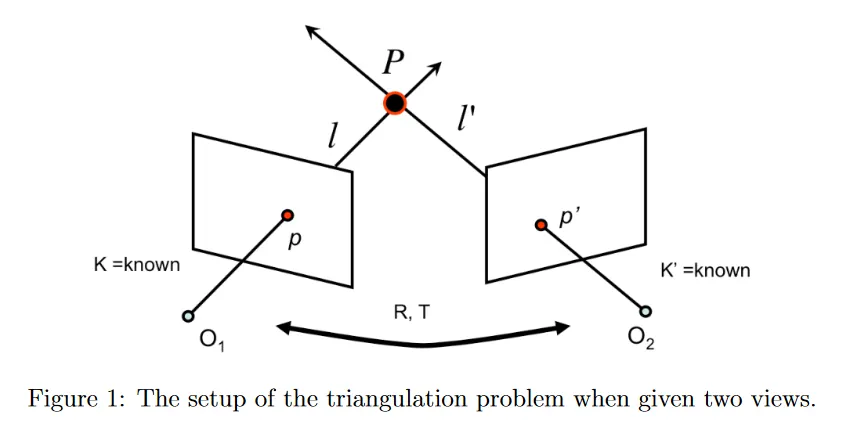
Triangulation

Triangulation(삼각측량)은 2개 이상의 이미지에 투영된 점을 바탕으로 3d 점의 위치를 결정하는 과정이다.
삼각측량에서 두 카메라 이미지가 rectified 일 때와 rectified가 아닐 때 사용하는 방법에 차이가 있는데, 두 이미지가 rectified 일 때는 매칭점 사이의 disparity를 통해 3d 점의 위치를 계산할 수 있고, rectified가 아닐 때는 아래 설명과 같이 카메라 투영행렬을 이용해서 3d 점의 위치를 계산할 수 있다.
일반적으로 이미지를 rectify 하는 비용 자체가 크기 때문에, 만일 카메라가 이동하거나 회전하는 일이 지속적으로 발생한다면 카메라 투영행렬을 이용하여 depth를 추출하고, 카메라가 고정된 상태라면 처음에 rectify를 수행한 후에 disparity만 이용하여 depth를 추출하는 것이 낫다.
두 대의 카메라에 대해 intrinsic K,K′K, K'와 두 카메라의 상대적인 회전과 평행이동인 R,TR, T을 안다고 하자. 3d 점 PP가 존재할 때 두 카메라 이미지에 대한 투영 점이 p,p′p, p'일 때, K,K′,R,TK, K', R, T가 알려져있고 카메라 중심 O1,O2O_1, O_2와 이미지 위치 p,p′p, p'에 의해 정의되는 시선 ℓ,ℓ′\ell, \ell'을 계산할 수 있으므로 PP를 두 시선 ℓ,ℓ′\ell, \ell'의 교점으로 계산할 수 있다.
이것은 매우 간단하고 수학적으로 타당해 보이지만, 실제로는 잘 작동하지 않는데, 관측치 p,p′p, p'가 noisy이고 camera calibration 파라미터가 정밀하지 않기 때문에 ℓ,ℓ′\ell, \ell'의 교차점을 찾는 것에 문제가 있다. 대부분의 경우 두 선이 교차하지 않아서 교점이 전혀 존재하지 않을 수도 있다.

A linear method for triangulation

우선 교점이 존재하지 않을 때를 해결하는 linear triangulation 방법을 살핀다. 3d 점을 이미지 평면에 투영하는 두 카메라의 projection matrix M,M′M, M'을 이용하여 서로 대응하는 두 이미지의 점이 p=MP=(x,y,1)p = MP = (x, y, 1)와 p′=M′P=(x′,y′,1)p' = M'P = (x', y', 1)으로 주어질 때, cross-product의 정의에 따라 p×(MP)=0p \times (MP) = 0이 된다. 이것을 이용하여 다음의 3가지 제약조건을 형성할 수 있다.
x(M3P)−(M1P)=0y(M3P)−(M2P)=0x(M2P)−y(M1P)=0\begin{aligned} x(M_3P) - (M_1P) &= 0 \\ y(M_3P) - (M_2P) &= 0 \\ x(M_2P) - y(M_1P) &= 0 \end{aligned}
여기서 MiM_i는 행렬 MM의 ii-번째 행이다. 유사한 제약조건을 p′p'와 M′M'에 대해서도 적용할 수 있다.
위의 두 이미지에 대한 제약조건에 대해 아래와 같이 AP=0AP = 0 형식의 선형 방정식을 만들 수 있다. (제약 조건에 대해 양변에 PP를 나누면 된다.) 여기서 AA는 다음 형식이 된다.
A=[xM3−M1yM3−M2x′M3′−M1′y′M3′−M2′]A = \begin{bmatrix} xM_3 - M_1 \\ yM_3 - M_2 \\ x'M_3' - M_1' \\ y'M_3' - M_2' \end{bmatrix}
이 등식은 SVD를 사용하여 해결될 수 있다. 이 방법의 또 다른 흥미로운 측면은 여러 view에서 triangulating을 잘 다룰 수 있다는 것이다. 그것을 하려면 새로운 view에 의해 추가되는 제약조건에 해당하는 행을 AA에 추가하면 된다.
그러나 이 방법은 간단하지만 projective-invariant가 아니므로 projective reconstruction에 적합하지 않고 따라서 triangulation 문제의 최적해가 아니다.

A nonlinear method for triangulation

현실에서 triangulation 문제는 다음의 최소화 문제를 해결하는 것으로 특성화 된다.
min⁡P^∥MP^−p∥2+∥M′P^−p′∥2\min_{\hat{P}}\|M\hat{P} - p\|^2 + \|M'\hat{P}-p'\|^2
두 이미지에 대해 P^\hat{P}의 reprojection error에 대한 least square를 찾아서 PP를 가장 잘 근사하는 3d 공간의 점 P^\hat{P}를 찾는다. 여기서 reprojection error는 실제 3d 점을 이미지에 projection 한 것과 이미지 평면에서 해당하는 점 사이의 거리가 된다. 이미지가 2개 이상인 경우 목적함수에 거리항을 더 추가하면 된다.
이 문제에 대한 좋은 근사치를 얻을 수 있는 다양한 최적화 방법이 존재하지만, Gauss-Newton Algorithm을 이용한다. 일반적인 nonlinear least square는 다음을 최소화하는 x∈Rnx \in \mathbb{R}^n을 찾는다.
∥r(x)∥2=∑i=1mri(x)2\|r(x)\|^2 = \sum_{i=1}^m r_i(x)^2
여기서 r:Rn→Rmr : \mathbb{R}^n \to \mathbb{R}^m은 residual function으로 어떤 함수 ff, 입력 xx와 관찰 yy에 대해 r(x)=f(x)−yr(x) = f(x) - y인 함수이다. 함수 ff가 선형이면 regular linear least square 문제로 축소된다. 일반적으로 카메라 행렬은 이미지 평면에 대한 projection을 homogeneous 좌표로 나누기 때문에 affine이 아니다. 따라서 이미지에 대한 projection은 일반적으로 비선형이다.
residual error eie_i를 2×12 \times 1 벡터 ei=MiP^−pie_i = M_i\hat{P} - p_i로 설정하면 최적화 문제를 다음과 같이 재형식화 할 수 있다.
min⁡P^∑iei(P^)2\min_{\hat{P}} \sum_i e_i(\hat{P})^2
이것은 완벽하게 nonlinear least squares 문제로 표현될 수 있다. Gauss-Newton algorithm을 사용하면 이 nonlinear least squares 문제에 대한 근사 해를 찾을 수 있다. 우선 선형 방법으로 계산될 수 있는 3d 점 P^\hat{P}에 대한 합리적인 추정치가 있다고 가정한다. Gauss-Newton algorithm은 reprojection error를 최소화하는 방향으로 현재 추정치를 보정하여 이것을 업데이트한다. 즉, 각 단계에서 추정치 P^\hat{P}를 어떤 δP:P^=P^+δP\delta_P : \hat{P} = \hat{P} + \delta_P만큼 업데이트한다.
그렇다면 업데이트 파라미터 δP\delta_P를 어떻게 선택할 수 있을까? Gauss-Newton 알고리즘의 핵심 통찰은 현재 추정치 P^\hat{P} 근처에서 residual 함수를 선형화하는 것이다. 위의 문제의 경우 이것은 점 PP의 residual error ee를 다음과 같이 생각할 수 있다는 것을 의미한다.
e(P^+δP)≈e(P^)+∂e∂PδPe(\hat{P} + \delta_P) \approx e(\hat{P}) + {\partial e \over \partial P} \delta_P
결과적으로 최소화 문제는 다음이 된다.
min⁡δP∥∂e∂PδP−(−e(P^))∥2\min_{\delta_P} \left\|{\partial e \over \partial P} \delta_P - (-e(\hat{P}))\right\|^2
이와 같이 residual을 형식화하면 표준 linear least squares 문제의 형식을 취하는 것을 볼 수 있다. NN개 이미지에 대한 triangulation 문제에 대해 linear least squares 해는 다음이 된다.
δP=−(J⊤J)−1J⊤e\delta_P = -(J^\top J)^{-1}J^\top e
여기서
e=[e1⋮eN]=[p1−M1P^⋮pn−MnP^]J=[∂e1∂P^1∂e1∂P^2∂e1∂P^3⋮∂eN∂P^1∂eN∂P^2∂eN∂P^3]\begin{aligned} e &= \begin{bmatrix} e_1 \\ \vdots \\ e_N \end{bmatrix} = \begin{bmatrix} p_1 - M_1\hat{P} \\ \vdots \\ p_n - M_n \hat{P} \end{bmatrix} \\ J &= \begin{bmatrix} {\partial e_1 \over \partial \hat{P}_1} & {\partial e_1 \over \partial \hat{P}_2} & {\partial e_1 \over \partial \hat{P}_3} \\ & \vdots \\ {\partial e_N \over \partial \hat{P}_1} & {\partial e_N \over \partial \hat{P}_2} & {\partial e_N \over \partial \hat{P}_3} \end{bmatrix} \end{aligned}
위 알고리즘을 고정된 단계 수나 수치적으로 수렴할 때까지 반복하면 된다. 다만 실제로는 수렴이 보장되지 않기 때문에 업데이트 횟수에 상한을 두는 것이 유용하다.
업데이트를 한다고 해서 파라미터를 학습한다는 것이 아니라, stereo 이미지에서 매칭된 모든 점에 대해 수렴할 때까지(또는 정해진 횟수)로 업데이트를 수행하는 것을 의미한다. 따라서 이 방법 그대로 실시간 응용에 사용하기는 어렵다.

Depth Estimation

만일 두 카메라의 이미지가 rectified라면 카메라 투영 행렬을 사용하지 않고 간편하게 3d 점을 구할 수 있다.
rectified라면 두 이미지의 행(또는 열)이 일치한 상태이므로 두 매칭점 사이의 수평(또는 수직)거리로 disparity를 정의할 수 있다. 즉 d=pu′−pud = p_u' - p_u이고 pu+d=pu′p_u + d = p_u'이다. (모든 PP에 대해 pu′>pup_u' > p_u 임에 유의하라). 만일 두 카메라가 수직으로 rectified 되었다면 disparity는 두 대응점 사이의 수직 거리가 된다.
그러면 disparity와 depth 사이에 간단한 반비례 관계가 있음을 볼 수 있다. 이것은 카메라 중심에 대한 PP의 zz-좌표로 정의된다. 그림 3에 나온대로 유사 삼각형을 사용하여 아래 식을 얻을 수 있다.
z=focal length×base linedisparityz = {\text{focal length} \times \text{base line} \over \text{disparity}}
만일 zz가 11이라고 가정한다면 disparity는 focal length와 baseline의 곱으로 표현할 수 있다.
z×disparity=focal length×base linez \times \text{disparity} = \text{focal length} \times \text{base line}
baseline은 두 카메라의 상대적인 평행이동(왼쪽 카메라를 기준으로 오른쪽 카메라의 평행이동)인 translation vector을 이용하여 다음과 같이 구할 수 있다.
baseline=tx2+ty2+tz2\text{baseline} = \sqrt{t_x^2 + t_y^2 + t_z^2}
focal length는 카메라의 intrinsic 파라미터를 이용해서 다음과 같이 구할 수 있다.
focal length=fx+fy2\text{focal length} = {f_x + f_y \over 2}
만일 두 카메라의 focal length가 다르다면 두 카메라의 focal length의 평균값을 사용한다.
pp에 대한 대응점 p′p'를 식별하는 한가지 접근은 다른 이미지에서 epipolar line을 따라 간단한 1d 검색을 수행하여 픽셀 또는 패치 유사성을 사용하여 가장 가능한 p′p'의 위치를 결정하는 것이다. 그러나 이런 순진한 접근은 현실 세계 이미지에서 occlusion, repetitive 패턴과 homogeneous region(즉, texture의 부재)과 같은 이슈를 겪을 수 있다. 따라서 현대의 representation learning 방법을 사용한다.

참고

Made with