Search
Duplicate

AI/ Flash Attention

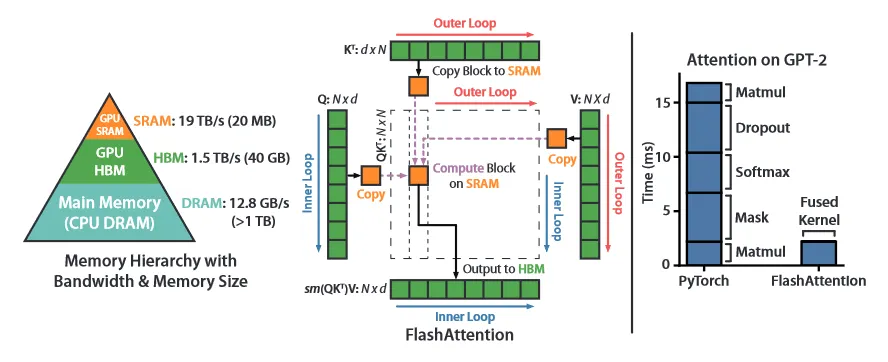
Flash Attention은 Transformer에서 병목으로 작용하는 Attention 부분에 대해 몇 가지 최적화 기법을 도입하여 성능을 높인 방법이다. 개념적으로 Flash Attention은 최신 GPU에서 연산 속도가 메모리 접근 속도를 압도하기 때문에 연산의 병목은 메모리 접근 —보다 정확히는 HBM 접근—에 있다는 아이디어에 착안하여, 메모리 접근을 줄이고, 대신 연산을 더 해서 전체 계산 속도를 높이는 방식을 취한다.
계산 자체는 원래의 Attention과 동일하므로 그 결과는 동일하지만, 하드웨어를 고려한(hardware-aware) 최적화로 성능(속도와 시퀀스 길이)을 높였기 때문에 Transformer를 사용하는 많은 곳에서 채택되었다. —추가로 메모리 관리를 효율화한 덕에 더 긴 시퀀스를 사용할 수 있게 되었고 결과적으로 품질 또한 더 좋아짐— Flash Attention이 최초로 제안 된 후에 해당 방법을 기반으로 하되 좀 더 개선한 Flash Attention 2가 등장했기 때문에 1, 2로 나누어 정리한다.

Flash Attention 1

Flash Attention 1의 하드웨어 측면에서 Attention의 계산의 최적화를 시도하는 접근으로, 이를 위해 GPU에서 실행의 병목인 HBM 접근을 최소화하고 대신 상대적으로 더 여유로운 연산을 (SRAM에서) 더 수행하여 전체 성능을 높인다는 아이디어를 사용한다. 간단한 GPU 메모리 계층 구조는 아래 그림 참조. (실제로 GPU에는 이 보다 다양한 메모리 계층 구조가 존재한다. 참고 부분 참조)
이것을 구현하기 위한 핵심 방법은 아래 2가지다.
1.
forward pass에서 softmax를 분할해서 계산하는 방법(이것을 Tiling이라 부름)
2.
forward pass에서 softmax의 정규화 상수를 저장한 다음에 backward pass에서 이를 활용하여 재계산하는 것(이것을 Recomputation이라 부름)
추가로 기존에 알고리즘 측면에서 Transformer의 성능을 높이는 시도들이 존재 했는데 —논문 저자에 의하면 유의미한 성과는 없었다고 함— 그런 방법들을 참조한 Block-Sparse Flash Attention도 시도한다.

Standard Attention

우선 표준 Attention의 연산은 다음과 같이 정의된다.
S=QK⊤∈RN×NP=softmax(S)∈RN×NO=PV∈RN×d\begin{aligned} \bold{S} &= \bold{QK}^\top \in \mathbb{R}^{N \times N} \\ \bold{P} &= \text{softmax}(\bold{S}) \in \mathbb{R}^{N \times N} \\ \bold{O} &= \bold{PV} \in \mathbb{R}^{N \times d} \end{aligned}
Q\bold{Q}와 K\bold{K}를 곱한 것에 softmax를 씌운 후 그 결과를 다시 V\bold{V}와 곱해서 출력 O\bold{O}를 만든다. 이 알고리즘에 대한 메모리 접근은 다음과 같다.
Algorithm. Standard Attention 구현
Require: HBM에 행렬 Q,K,V∈RN×d\bold{Q}, \bold{K}, \bold{V} \in \mathbb{R}^{N\times d}
1.
HBM에서 block 별로 Q,K\bold{Q}, \bold{K}를 로드, S=QK⊤\bold{S} = \bold{QK}^\top를 계산, S\bold{S}를 HBM에 씀
2.
HBM에서 S\bold{S}를 읽고, P=softmax(S)\bold{P} = \text{softmax}(\bold{S})를 계산, P\bold{P}를 HBM에 씀
3.
HBM에서 block 별로 P\bold{P}와 V\bold{V}를 로드, O=PV\bold{O} = \bold{PV}를 계산 O\bold{O}를 HBM에 씀
4.
O\bold{O} 반환
기존 Attention 계산은 크기가 큰 행렬을 HBM에 저장하고, 연산 단계마다 해당 행렬을 처리하기 위해 HBM 접근을 수행하는데, 이것이 전체 성능의 병목이 된다.

Forward Pass

표준 Attention 방법의 성능을 개선하기 위해 softmax 계산을 분할해서 처리해야 한다. 우선 수치적 안정성을 위해 softmax를 다음과 같이 각 행별로 max⁡\max 값을 찾아서 각 항목에서 빼는 형식으로 계산한다.
m(x):=max⁡ixif(x):=[ex1−m(x)...exB−m(x)]ℓ(x):=∑if(x)isoftmax(x):=f(x)ℓ(x)\begin{aligned} m(x) &:= \max_i x_i \\ f(x) &:= [e^{x_1-m(x) } \quad ... \quad e^{x_B - m(x)}] \\ \ell(x) &:= \sum_i f(x)_i \\ \text{softmax}(x) &:= {f(x) \over \ell(x)} \end{aligned}
여기서 f(x)f(x)는 개별 항목을 max⁡\max로 뺀 후에 exp⁡\exp를 씌운 결과이며 ℓ(x)\ell(x)는 전체 f(x)f(x)를 합한 정규화 상수이다. 최종적으로 softmax의 정의대로 각 f(x)f(x)를 정규화 상수 ℓ(x)\ell(x)로 나누어 계산한다.
위와 같이 정의된 softmax 계산을 다음처럼 분할하여 처리할 수 있다. 단순한 예로 벡터 x=[x(1)x(2)]∈R2Bx = [x^{(1)} \quad x^{(2)}] \in \mathbb{R}^{2B}에 대해 (여기서 x(1),x(2)∈RBx^{(1)}, x^{(2)} \in \mathbb{R}^B) softmax를 다음과 같이 분해하여 계산할 수 있다.
m(x)=m([x(1)x(2)])=max⁡(m(x(1)),m(x(2)))f(x)=[em(x(1))−m(x)f(x(1))em(x(2))−m(x)f(x(2))]ℓ(x)=ℓ([x(1)x(2)])=em(x(1))−m(x)ℓ(x(1))+em(x(2))−m(x)ℓ(x(2))softmax(x)=f(x)ℓ(x)\begin{aligned} m(x) &= m( [x^{(1)} \quad x^{(2)}]) = \max(m(x^{(1)}), m(x^{(2)})) \\ f(x) &= [e^{m(x^{(1)}) - m(x)}f(x^{(1)}) \quad e^{m(x^{(2)})-m(x)}f(x^{(2)}) ] \\ \ell(x) &= \ell([x^{(1)} \quad x^{(2)}]) = e^{m(x^{(1)})-m(x)}\ell(x^{(1)}) + e^{m(x^{(2)}) - m(x)}\ell(x^{(2)}) \\ \text{softmax}(x) &= {f(x) \over\ell(x)}\end{aligned}
여기서 f(x)f(x)와 ℓ(x)\ell(x)에 대한 유도는 아래 페이지의 3.1 부분 참조
기본 절차에 Mask와 dropout을 포함한 Attention의 forward 전체 알고리즘은 다음과 같다. backward pass를 위해 여기서 계산한 softmax의 정규화 통계량 (m,ℓ)(m, \ell)과 랜덤 난수 생성기 R\mathcal{R}를 저장한다.
Algorithm - FlashAttention Forward Pass
Require: HBM에서 행렬 Q,K,V∈RN×d\bold{Q}, \bold{K}, \bold{V} \in \mathbb{R}^{N\times d}, 크기 MM의 on-chip SRAM, softmax scaling 상수 τ∈R\tau \in \mathbb{R}, masking 함수 MASK\text{MASK}, dropout 확률 pdropp_\text{drop}
1.
pseudo-random number 생성기 상태 R\mathcal{R}을 초기화하고 HBM에 저장
2.
block 크기 Bc=⌈M4d⌉,Br=min⁡(⌈M4d⌉,d)B_c = \lceil{M \over 4d} \rceil, B_r = \min(\lceil{M \over 4d}\rceil, d) 설정
3.
HBM에 O=(0)N×d∈RN×d,ℓ=(0)N∈RN,m=(−∞)N∈RN\bold{O} = (0)_{N \times d} \in \mathbb{R}^{N \times d}, \ell = (0)_N \in \mathbb{R}^N, m = (-\infty)_N \in \mathbb{R}^N 초기화
4.
Q\bold{Q}를 각각 Br×dB_r \times d 크기의 Tr=⌈NBr⌉T_r = \lceil {N \over B_r} \rceil개 블록 Q1,...,QT\bold{Q}_1, ..., \bold{Q}_T으로 분할하고, K,V\bold{K}, \bold{V}를 각각 Bc×dB_c \times d 크기의 Tc=⌈NBc⌉T_c = \lceil {N \over B_c} \rceil개 블록 K1,...,KTc\bold{K}_1, ..., \bold{K}_{T_c}과 V1,...,VTc\bold{V}_1, ..., \bold{V}_{T_c}으로 분할
5.
O\bold{O}를 각각 Br×dB_r \times d 크기의 TrT_r개 블록 Oi,...,OTr\bold{O}_i,..., \bold{O}_{T_r}로 분할, ℓ\ell을 각각 BrB_r 크기의 TrT_r개 블록 ℓi,...,ℓTr\ell_i,...,\ell_{T_r}로 분할 mm을 각각 BrB_r 크기의 TrT_r개 블록 m1,...,mTrm_1,..., m_{T_r}로 분할
6.
for 1≤j≤Tc1 \le j \le T_c do
a.
Kj,Vj\bold{K}_j, \bold{V}_j를 HBM에서 on-chip SRAM으로 로드
b.
for 1≤i≤Tr1 \le i \le T_r do
i.
Qi,Oi,ℓi,mi\bold{Q}_i, \bold{O}_i, \ell_i, m_i를 HBM에서 on-chip SRAM으로 로드
ii.
On chip에서 Sij=τQiKj⊤∈RBr×Bc\bold{S}_{ij} = \tau \bold{Q}_i \bold{K}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산
iii.
On chip에서 Sijmasked=MASK(Sij)\bold{S}_{ij}^\text{masked} = \text{MASK}(\bold{S}_{ij}) 계산
iv.
On chip에서 다음을 계산
•
m~ij=rowmax(Sijmasked)∈RBr\tilde{m}_{ij} = \text{rowmax}(\bold{S}_{ij}^\text{masked}) \in \mathbb{R}^{B_r}
•
P~ij=exp⁡(Sijmasked−m~ij)∈RBr×Bc\tilde{\bold{P}}_{ij} = \exp(\bold{S}_{ij}^\text{masked} - \tilde{m}_{ij}) \in \mathbb{R}^{B_r \times B_c} (pointwise)
•
ℓ~ij=rowsum(P~ij)∈RBr\tilde{\ell}_{ij} = \text{rowsum}(\tilde{\bold{P}}_{ij}) \in \mathbb{R}^{B_r}
v.
On chip에서 다음을 계산
•
minew=max⁡(mi,m~ij)∈RBrm_i^\text{new} = \max(m_i, \tilde{m}_{ij}) \in \mathbb{R}^{B_r}
•
ℓinew=emi−minewℓi+em~ij−minewℓ~ij∈RBr\ell_i^\text{new} = e^{m_i - m_i^\text{new}}\ell_i + e^{\tilde{m}_{ij} - m_i^\text{new}}\tilde{\ell}_{ij} \in \mathbb{R}^{B_r}
vi.
On chip에서 P~ijdropped=dropout(P~ij,pdrop)\tilde{\bold{P}}_{ij}^\text{dropped} = \text{dropout}(\tilde{\bold{P}}_{ij},p_\text{drop})
vii.
HBM에 Oi←diag(ℓinew)−1(diag(ℓi)emi−minewOi+em~ij−minewP~ijdroppedVj)\bold{O}_i \leftarrow \text{diag}(\ell_i^\text{new})^{-1}(\text{diag}(\ell_i)e^{m_i - m_i^\text{new}}\bold{O}_i + e^{\tilde{m}_{ij} - m_i^\text{new}}\tilde{\bold{P}}_{ij}^\text{dropped}\bold{V}_j) 쓰기
viii.
HBM에 ℓi←ℓinew,mi←minew\ell_i \leftarrow \ell_i^\text{new}, m_i \leftarrow m_i^\text{new} 쓰기
c.
end for
7.
end for
8.
O,ℓ,m,R\bold{O}, \ell, m, \mathcal{R} 반환

Backward Pass

Backward pass는 다음과 같이 Forward pass의 반대 방향으로 계산한다. 여기서 d\bold{d}는 각 항목의 gradient를 의미한다.
dV=P⊤dO∈RN×ddP=dOV⊤∈RN×NdS=dsoftmax(dP)∈RN×NdQ=dSK∈RN×ddK=QdS⊤∈RN×d\begin{aligned} \bold{dV} &= \bold{P}^\top \bold{dO} \in \mathbb{R}^{N \times d} \\ \bold{dP} &= \bold{dOV}^\top \in \mathbb{R}^{N \times N} \\ \bold{dS} &= \text{dsoftmax}(\bold{dP}) \in \mathbb{R}^{N \times N} \\ \bold{dQ} &= \bold{dSK} \in \mathbb{R}^{N \times d} \\ \bold{dK} &= \bold{QdS}^\top \in \mathbb{R}^{N \times d} \end{aligned}
원래는 forward에서 계산된 출력 O\bold{O}을 load하여 gradient를 계산하지만, Flash Attention에서는 HBM 접근을 최소화 하기 위해 Backward pass에서 이 O\bold{O}을 아예 다시 계산한다 (이것을 recomputation이라 부름). 이때 forward pass에서 계산된 softmax 통계량 (m,ℓ)(m, \ell)을 이용한다. —이것도 메모리를 사용하지만 O\bold{O} 전체를 load 하는 것보다는 낫다.
backward에서 필요한 몇 가지 gradient를 구하는 상세한 내용은 아래 페이지의 B.2 부분 참조
Recomputation과 gradient 계산을 포함하여 Backward pass의 전체 알고리즘은 다음과 같다.
Algorithm - FlashAttention Backward pass
Require: HBM에서 행렬 Q,K,V,dO∈RN×d\bold{Q}, \bold{K}, \bold{V}, \bold{dO} \in \mathbb{R}^{N \times d}, HBM에서 벡터 ℓ,m∈RN\ell, m \in \mathbb{R}^N, 크기 MM의 on-chip SRAM, softmax scaling 상수 τ∈R\tau \in \mathbb{R}, masking 함수 MASK\text{MASK}, dropout 확률 pdropp_\text{drop}, forward pass에서 pseudo-random number 생성기 상태 R\mathcal{R}
1.
pseudo-random number 생성기 상태를 R\mathcal{R}로 설정
2.
block 크기 Bc=⌈M4d⌉,Br=min⁡(⌈M4d⌉,d)B_c = \lceil{M \over 4d} \rceil, B_r = \min(\lceil{M \over 4d}\rceil, d) 설정
3.
Q\bold{Q}를 각각 Br×dB_r \times d 크기의 Tr=⌈NBr⌉T_r = \lceil {N \over B_r} \rceil개 블록 Q1,...,QT\bold{Q}_1, ..., \bold{Q}_T으로 분할하고, K,V\bold{K}, \bold{V}를 각각 Bc×dB_c \times d 크기의 Tc=⌈NBc⌉T_c = \lceil {N \over B_c} \rceil개 블록 K1,...,KTc\bold{K}_1, ..., \bold{K}_{T_c}과 V1,...,VTc\bold{V}_1, ..., \bold{V}_{T_c}으로 분할
4.
O\bold{O}를 각각 Br×dB_r \times d 크기의 TrT_r개 블록 Oi,...,OTr\bold{O}_i,..., \bold{O}_{T_r}로 분할, dO\bold{dO}를 각각 Br×dB_r \times d 크기의 TrT_r개 블록 dOi,...,dOTr\bold{dO}_i, ..., \bold{dO}_{T_r}로 분할, ℓ\ell을 각각 BrB_r 크기의 TrT_r개 블록 ℓi,...,ℓTr\ell_i,...,\ell_{T_r}로 분할 mm을 각각 BrB_r 크기의 TrT_r개 블록 m1,...,mTrm_1,..., m_{T_r}로 분할
5.
HBM에서 dQ=(0)N×d\bold{dQ} = (0)_{N\times d}를 초기화하고 각각 Br×dB_r \times d 크기의 TrT_r 블록 dQ1,...,dQTr\bold{dQ}_1,..., \bold{dQ}_{T_r}로 분할. HBM에서 dK=(0)N×d,dV=(0)N×d\bold{dK} = (0)_{N\times d}, \bold{dV} = (0)_{N \times d}를 초기화하고 각각 Bc×dB_c \times d 크기의 TcT_c개 블록 dK1,...,dKTc\bold{dK}_1,..., \bold{dK}_{T_c}와 dV1,...,dVTc\bold{dV}_1,..., \bold{dV}_{T_c}로 분할.
6.
for i≤j≤Tci \le j \le T_c do
a.
HBM에서 on-chip SRAM으로 Kj,Vj\bold{K}_j, \bold{V}_j 로드
b.
SRAM에서 dK~j=(0)Bc×d,dV~j=(0)Bc×d\bold{d}\tilde{\bold{K}}_j = (0)_{B_c \times d}, \bold{d}\tilde{\bold{V}}_j = (0)_{B_c \times d} 초기화
c.
for 1≤i≤Tr1 \le i \le T_r do
i.
HBM에서 on-chip SRAM으로 Qi,Oi,dOi,dQi,ℓi,mi\bold{Q}_i, \bold{O}_i, \bold{dO}_i, \bold{dQ}_i, \ell_i, m_i 로드
ii.
On chip에서 Sij=τQiKj⊤∈RBr×Bc\bold{S}_{ij} = \tau\bold{Q}_i\bold{K}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산
iii.
On chip에서 Sijmasked=MASK(Sij)\bold{S}_{ij}^\text{masked} = \text{MASK}(\bold{S}_{ij}) 계산
iv.
On chip에서 Pij=diag(ℓi)−1exp⁡(Sijmasked−mi)∈RBr×Bc\bold{P}_{ij} = \text{diag}(\ell_i)^{-1}\exp(\bold{S}_{ij}^\text{masked} - m_i) \in \mathbb{R}^{B_r \times B_c} 계산
v.
On chip에서 dropout mask Zij∈RBr×Bc\bold{Z}_{ij} \in \mathbb{R}^{B_r \times B_c} 계산. 여기서 각 항은 1−pdrop1- p_\text{drop}의 확률로 11−pdrop{1\over 1- p_\text{drop}}의 값을 갖고 pdropp_\text{drop}의 확률로 00의 값을 가짐
vi.
On chip에서 Pijdropped=Pij∘Zij\bold{P}_{ij}^\text{dropped} = \bold{P}_{ij} \circ \bold{Z}_{ij} 계산 (pointwise 곱)
vii.
On chip에서 dV~j←dV~j+(Pijdropped)⊤dOi∈RBc×d\bold{d}\tilde{\bold{V}}_j \leftarrow \bold{d}\tilde{\bold{V}}_j + (\bold{P}_{ij}^\text{dropped})^\top \bold{dO}_i \in \mathbb{R}^{B_c \times d} 계산
viii.
On chip에서 dPijdropped=dOiVj⊤∈RBr×Bc\bold{dP}_{ij}^\text{dropped} = \bold{dO}_i \bold{V}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산
ix.
On chip에서 dPij=dPijdropped∘Zij\bold{dP}_{ij} = \bold{dP}_{ij}^\text{dropped} \circ \bold{Z}_{ij} 계산 (pointwise 곱)
x.
On chip에서 Di=rowsum(dOi∘Oi)∈RBrD_i = \text{rowsum}(\bold{dO}_i \circ \bold{O}_i) \in \mathbb{R}^{B_r} 계산
xi.
On chip에서 dSij=Pij∘(dPij−Di)∈RBr×Bc\bold{dS}_{ij} = \bold{P}_{ij} \circ (\bold{dP}_{ij} - D_i) \in \mathbb{R}^{B_r \times B_c} 계산
xii.
HBM으로 dQi←dQi+τdSijKj∈RBr×d\bold{dQ}_i \leftarrow \bold{dQ}_i + \tau\bold{dS}_{ij}\bold{K}_j \in \mathbb{R}^{B_r \times d} 쓰기
xiii.
On chip에서 dK~j←dK~j+τdSij⊤Qi∈RBc×d\bold{d}\tilde{\bold{K}}_j \leftarrow \bold{d}\tilde{\bold{K}}_j + \tau \bold{dS}_{ij}^\top \bold{Q}_i \in \mathbb{R}^{B_c \times d} 계산
d.
end for
e.
HBM으로 dKj←dK~j,dVj←dV~j\bold{dK}_j \leftarrow \bold{d}\tilde{\bold{K}}_j, \bold{dV}_j \leftarrow \bold{d}\tilde{\bold{V}}_j 쓰기
7.
end for
8.
dQ,dK,dV\bold{dQ}, \bold{dK}, \bold{dV} 반환

Block-Sparse

알고리즘 측면에서 Attention 성능 개선을 시도했던 기존 방법들을 참조하여 표준 Attention에 대해 다음과 같이 block-sparse를 도입한 block-sparse FlashAttention을 정의한다. 이것은 Flash Attention 보다도 훨씬 빠르다. —물론 sparse로 만들면서 품질에 대해 trade-off가 발생할 수 있음
S=QK⊤∈RN×NP=softmax(S⊙1M~)∈RN×NO=PV∈RN×d\begin{aligned} \bold{S} &= \bold{QK}^\top \in \mathbb{R}^{N \times N} \\ \bold{P} &= \text{softmax}(\bold{S} \odot \bold{1}_{\tilde{\bold{M}}}) \in \mathbb{R}^{N \times N} \\ \bold{O} &= \bold{PV} \in \mathbb{R}^{N \times d} \end{aligned}
여기서 M~∈{0,1}N×N\tilde{\bold{M}} \in \{0, 1\}^{N \times N}는 블록 형태의 mask 행렬로, M~kl=1\tilde{\bold{M}}_{kl} = 1이면 (S⊙1M~)kl=Skl(\bold{S} \odot\bold{1}_{\tilde{\bold{M}}})_{kl} = \bold{S}_{kl}이고 Mkl=0\bold{M}_{kl} = 0이면 −∞-\infty이다.
미리 정의된 block sparsity mask M∈{0,1}N/Br×N/Bc\bold{M} \in \{0, 1\}^{N/B_r \times N/B_c}가 주어지면 attention 행렬의 non-zero 블록만 쉽게 계산할 수 있다. 이것은 forward pass 알고리즘과 유사하지만 zero 블록을 skip 한다.
Block-sparse 버전의 Forward pass 전체 알고리즘은 다음과 같다.
Algorithm - Block-Sparse FlashAttention Forward Pass
Require: HBM에서 행렬 Q,K,V,dO∈RN×d\bold{Q}, \bold{K}, \bold{V}, \bold{dO} \in \mathbb{R}^{N \times d}, 크기 MM의 on-chip SRAM, softmax scaling 상수 τ∈R\tau \in \mathbb{R}, masking 함수 MASK\text{MASK}, dropout 확률 pdropp_\text{drop}, block size Bc=⌈M4D⌉,Br=min⁡(⌈M4d⌉,d)B_c = \lceil{M \over 4D} \rceil, B_r = \min(\lceil{M \over 4d}\rceil, d), block sparsity mask M∈{0,1}N/Br×N/BcM \in \{ 0, 1\}^{N/B_r \times N/B_c}
1.
pseudo-random number 생성기 상태를 R\mathcal{R}로 설정하고 HBM으로 저장
2.
HBM에서 O=(0)N×d∈RN×d,ℓ=(0)N∈RN,m=(−∞)N∈RN\bold{O} = (0)_{N \times d} \in \mathbb{R}^{N \times d}, \ell=(0)_N \in \mathbb{R}^N, m = (-\infty)_N \in \mathbb{R}^N 초기화
3.
Q\bold{Q}를 각각 Br×dB_r \times d 크기의 Tr=⌈NBr⌉T_r = \lceil {N \over B_r} \rceil개 블록 Q1,...,QT\bold{Q}_1, ..., \bold{Q}_T으로 분할하고, K,V\bold{K}, \bold{V}를 각각 Bc×dB_c \times d 크기의 Tc=⌈NBc⌉T_c = \lceil {N \over B_c} \rceil개 블록 K1,...,KTc\bold{K}_1, ..., \bold{K}_{T_c}과 V1,...,VTc\bold{V}_1, ..., \bold{V}_{T_c}으로 분할
4.
O\bold{O}를 각각 Br×dB_r \times d 크기의 TrT_r개 블록 Oi,...,OTr\bold{O}_i,..., \bold{O}_{T_r}로 분할, ℓ\ell을 각각 BrB_r 크기의 TrT_r개 블록 ℓi,...,ℓTr\ell_i,...,\ell_{T_r}로 분할 mm을 각각 BrB_r 크기의 TrT_r개 블록 m1,...,mTrm_1,..., m_{T_r}로 분할
5.
for i≤j≤Tci \le j \le T_c do
a.
HBM에서 on-chip SRAM으로 Kj,Vj\bold{K}_j, \bold{V}_j 로드
b.
for 1≤i≤Tr1 \le i \le T_r do
i.
if Mij≠0M_{ij} \ne 0 then
1.
HBM에서 on-chip SRAM으로 Qi,Oi,ℓi,mi\bold{Q}_i, \bold{O}_i, \ell_i, m_i 로드
2.
On chip에서 Sij=τQiKj⊤∈RBr×Bc\bold{S}_{ij} = \tau\bold{Q}_i\bold{K}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산
3.
On chip에서 Sijmasked=MASK(Sij)\bold{S}_{ij}^\text{masked} = \text{MASK}(\bold{S}_{ij}) 계산
4.
On chip에서 다음을 계산
•
m~ij=rowmax(Sijmasked)∈RBr\tilde{m}_{ij} = \text{rowmax}(\bold{S}_{ij}^\text{masked}) \in \mathbb{R}^{B_r}
•
P~ij=exp⁡(Sijmasked−m~ij)∈RBr×Bc\tilde{\bold{P}}_{ij} = \exp(\bold{S}_{ij}^\text{masked} - \tilde{m}_{ij}) \in \mathbb{R}^{B_r \times B_c} (pointwise)
•
ℓ~ij=rowsum(P~ij)∈RBr\tilde{\ell}_{ij} = \text{rowsum}(\tilde{\bold{P}}_{ij}) \in \mathbb{R}^{B_r}
5.
On chip에서 다음을 계산
•
minew=max⁡(mi,m~ij)∈RBrm_i^\text{new} = \max(m_i, \tilde{m}_{ij}) \in \mathbb{R}^{B_r}
•
ℓinew=emi−minewℓi+em~ij−minewℓ~ij∈RBr\ell_i^\text{new} = e^{m_i - m_i^\text{new}}\ell_i + e^{\tilde{m}_{ij} - m_i^\text{new}}\tilde{\ell}_{ij} \in \mathbb{R}^{B_r}
6.
On chip에서 P~ijdropped=dropout(P~ij,pdrop)\tilde{\bold{P}}_{ij}^\text{dropped} = \text{dropout}(\tilde{\bold{P}}_{ij},p_\text{drop})
7.
HBM에 Oi←diag(ℓinew)−1(diag(ℓi)emi−minewOi+em~ij−minewP~ijdroppedVj)\bold{O}_i \leftarrow \text{diag}(\ell_i^\text{new})^{-1}(\text{diag}(\ell_i)e^{m_i - m_i^\text{new}}\bold{O}_i + e^{\tilde{m}_{ij} - m_i^\text{new}}\tilde{\bold{P}}_{ij}^\text{dropped}\bold{V}_j) 쓰기
8.
HBM에 ℓi←ℓinew,mi←minew\ell_i \leftarrow \ell_i^\text{new}, m_i \leftarrow m_i^\text{new} 쓰기
ii.
end if
c.
end for
6.
end for
7.
O,ℓ,m,R\bold{O}, \ell, m, \mathcal{R} 반환

Flash Attention 2

Flash Attention 2은 FlashAttention 1이 이론적 최대 FLOPs/s의 25-40% 밖에 도달 못했기 때문에 그것을 더욱 개선한 버전이다. 저자들은 Flash Attention 1의 한계가 GPU의 다른 thread 블록과 warps 사이의 분할 작업이 suboptimal이기 때문에, 점유율이 낮고 불필요한 shared 메모리 읽기/쓰기가 발생한다고 관찰했고, 이를 개선하기 위해 다음의 3가지 방법을 도입하였다.
1.
기존 Flash Attention 알고리즘을 개선해서 non-Matmul FLOPs의 수를 줄임
•
GPU는 Matmul 연산에 특화된 유닛이 있기 때문에 최대한 Matmul을 사용하는 것이 유리하다. Matmul 처리량이 non-Matmul 처리량에 비해 16배 높다고 함
2.
점유율을 높이기 위해 단일 head에 대해서도 attention 계산을 다른 thread block에 병렬화
•
batch와 head 차원 외에 시퀀스 길이 차원을 따라 forward pass, backward pass를 모두 병렬화하여 GPU의 점유율을 높인다.
3.
각 thread block 내의 wraps 사이의 작업을 분배해서 shared 메모리를 통한 커뮤니케이션을 줄임.

Online Softmax

우선 기존의 Flash Attention의 forward 계산을 다음의 예처럼 계산할 수 있다. 여기서 S=[S(1)S(2)]\bold{S} = \begin{bmatrix} \bold{S}^{(1)} & \bold{S}^{(2)} \end{bmatrix}이고 V=[V(1)V(2)]\bold{V} = \begin{bmatrix} \bold{V}^{(1)} \\ \bold{V}^{(2)} \end{bmatrix}이다.
m=max⁡(rowmax(S(1)),rowmax(S(2)))∈RBrℓ=rowsum(eS(1)−m)+rowsum(eS(2)−m)∈RBrP=[P(1)P(2)]=diag(ℓ)−1[eS(1)−meS(2)−m]∈RBr×2BcO=[P(1)P(2)][V(1)V(2)]=diag(ℓ)−1(eS(1)−mV(1)+eS(2)−mV(2))∈RBr×d\begin{aligned} m &= \max(\text{rowmax}(\bold{S}^{(1)}), \text{rowmax}(\bold{S}^{(2)})) \in \mathbb{R}^{B_r} \\ \ell &= \text{rowsum}(e^{\bold{S}^{(1)}-m}) + \text{rowsum}(e^{\bold{S}^{(2)}-m}) \in \mathbb{R}^{B_r} \\ \bold{P} &= \begin{bmatrix} \bold{P}^{(1)} & \bold{P}^{(2)}\end{bmatrix} = \text{diag}(\ell)^{-1} \begin{bmatrix} e^{\bold{S}^{(1)} - m} & e^{\bold{S}^{(2)}-m} \end{bmatrix} \in \mathbb{R}^{B_r \times 2B_c} \\ \bold{O} &= \begin{bmatrix} \bold{P}^{(1)} & \bold{P}^{(2)} \end{bmatrix} \begin{bmatrix} \bold{V}^{(1)} \\ \bold{V}^{(2)}\end{bmatrix} =\text{diag}(\ell)^{-1} \left(e^{\bold{S}^{(1)}-m}\bold{V}^{(1)} + e^{\bold{S}^{(2)}-m}\bold{V}^{(2)} \right) \in \mathbb{R}^{B_r \times d} \end{aligned}
주의) 이것은 논문에 나온 설명을 따라 정리한 것인데, 본래 Flash Attention 1의 논문에서도 P\bold{P}를 먼저 구하고 그걸 합해서 ℓ\ell을 구하는데 여기서는 순서가 반대로 나온다. 실제로 Flash Attention 2의 forward 알고리즘에서도 P\bold{P}를 먼저 구함.
위의 방법에 대해 online softmax를 다음과 같이 계산할 수 있다. 각 블록에 대해 ‘local’ softmax를 계산한 후에 마지막에 rescale하여 올바른 결과를 얻는다.
m(1)=rowmax(S(1))∈RBrℓ(1)=rowsum(eS(1)−m(1))∈RBrP~(1)=diag(ℓ(1))−1eS(1)−m(1)∈RBr×BcO(1)=P~(1)V(1)=diag(ℓ(1))−1eS(1)−m(1)V(1)∈RBr×dm(2)=max⁡(m(1),rowmax(S(2)))=mℓ(2)=em(1)−m(2)ℓ(1)+rowsum(eS(2)−m(2))=rowsum(eS(1)−m)+rowsum(eS(2)−m)=ℓP~(2)=diag(ℓ(2))−1eS(2)−m(2)O(2)=diag(ℓ(1)/ℓ(2))−1O(1)+P~(2)V(2)=diag(ℓ(1))−1eS(1)−mV(1)+diag(ℓ(2))−1eS(2)−mV(2)=O\begin{aligned} m^{(1)} &= \text{rowmax}(\bold{S}^{(1)}) \in \mathbb{R}^{B_r} \\ \ell^{(1)} &= \text{rowsum}(e^{\bold{S}^{(1)}-m^{(1)}}) \in \mathbb{R}^{B_r} \\ \tilde{\bold{P}}^{(1)} &= \text{diag}(\ell^{(1)})^{-1} e^{\bold{S}^{(1)}-m^{(1)}} \in \mathbb{R}^{B_r \times B_c} \\ \bold{O}^{(1)} &= \tilde{\bold{P}}^{(1)}\bold{V}^{(1)} = \text{diag}(\ell^{(1)})^{-1} e^{\bold{S}^{(1)}-m^{(1)}}\bold{V}^{(1)} \in \mathbb{R}^{B_r \times d} \\ m^{(2)} &= \max(m^{(1)},\text{rowmax}(\bold{S}^{(2)})) = m \\ \ell^{(2)} &= e^{m^{(1)}-m^{(2)}}\ell^{(1)} + \text{rowsum}(e^{\bold{S}^{(2)} - m^{(2)}}) \\ & = \text{rowsum}(e^{\bold{S}^{(1)} - m}) + \text{rowsum}(e^{\bold{S}^{(2)}-m}) = \ell \\ \tilde{\bold{P}}^{(2)} &= \text{diag}(\ell^{(2)})^{-1}e^{\bold{S}^{(2)}-m^{(2)}} \\ \bold{O}^{(2)} &= \text{diag}(\ell^{(1)}/\ell^{(2)})^{-1}\bold{O}^{(1)} + \tilde{\bold{P}}^{(2)}\bold{V}^{(2)} \\&= \text{diag}(\ell^{(1)})^{-1}e^{\bold{S}^{(1)}-m}\bold{V}^{(1)} +\text{diag}(\ell^{(2)})^{-1}e^{\bold{S}^{(2)}-m}\bold{V}^{(2)} = \bold{O} \end{aligned}
주의) 원래 논문에서 마지막 줄은 diag(ℓ(2))−1eS(1)−mV(1)+diag(ℓ(2))−1eS(2)−mV(2)=O\text{diag}(\ell^{(2)})^{-1}e^{\bold{S}^{(1)}-m}\bold{V}^{(1)} +\text{diag}(\ell^{(2)})^{-1}e^{\bold{S}^{(2)}-m}\bold{V}^{(2)} = \bold{O} 로 되어 있는데, 오타 같아 보여서 ℓ(2)\ell^{(2)}를 ℓ(1)\ell^{(1)}으로 수정 함.

Forward Pass

위의 online 버전을 기준으로 non-Matmul FLOPs를 줄이기 위해 다음의 2가지 수정을 한다.
1.
출력 업데이트의 두 항을 diag(ℓ(2))−1\text{diag}(\ell^{(2)})^{-1}로 rescale 하지 않는다.
O(2)=diag(ℓ(1)/ℓ(2))−1O(1)+diag(ℓ(2))−1eS(2)−m(2)V(2)\bold{O}^{(2)} = \text{diag}(\ell^{(1)} / \ell^{(2)})^{-1} \bold{O}^{(1)} + \text{diag}(\ell^{(2)})^{-1} e^{\bold{S}^{(2)}-m^{(2)}}\bold{V}^{(2)}
대신 O(2)\bold{O}^{(2)}의 ‘un-scaled’ 버전을 유지하고 ℓ(2)\ell^{(2)}의 통계량을 유지할 수 있다.
O~(2)=diag(ℓ(1))−1O(1)+eS(2)−m(2)V(2)\tilde{\bold{O}}^{(2)} = \text{diag}(\ell^{(1)})^{-1} \bold{O}^{(1)} + e^{\bold{S}^{(2)}-m^{(2)}}\bold{V}^{(2)}
각 반복문의 끝에서만 최종 O~(last)\tilde{\bold{O}}^\text{(last)}를 diag(ℓ(last))−1\text{diag}(\ell^\text{(last)})^{-1}로 scale하여 올바른 결과를 얻는다.
2.
backward pass에 대해 최대 m(j)\bold{m}^{(j)}와 지수합 ℓ(j)\ell^{(j)}를 저장하지 않는다. 오직 log-sum-exp L(j)=m(j)+log⁡(ℓ(j))L^{(j)} = m^{(j)} + \log(\ell^{(j)})만 저장한다.
•
log-sum-exp를 적용한 방법의 유도는 AI/ Paper/ Flash Attention 2 참조.
위의 online softmax 예시에 대해 이 2가지 개선을 적용하면 다음과 같다.
m(1)=rowmax(S(1))∈RBrℓ(1)=rowsum(eS(1)−m(1))∈RBrO~(1)=eS(1)−m(1)V(1)∈RBr×dm(2)=max⁡(m(1),rowmax(S(2)))=mℓ(2)=em(1)−m(2)ℓ(1)+rowsum(eS(2)−m(2))=rowsum(eS(1)−m)+rowsum(eS(2)−m)=ℓP~(2)=diag(ℓ(2))−1eS(2)−m(2)O~(2)=diag(em(1)−m(2))O~(1)+eS(2)−m(2)V(2)=eS(1)−mV(1)+eS(2)−mV(2)O(2)=diag(ℓ(2))−1O~(2)=O\begin{aligned} m^{(1)} &= \text{rowmax}(\bold{S}^{(1)}) \in \mathbb{R}^{B_r} \\ \ell^{(1)} &= \text{rowsum}(e^{\bold{S}^{(1)}-m^{(1)}}) \in \mathbb{R}^{B_r} \\ \tilde{\bold{O}}^{(1)} &= e^{\bold{S}^{(1)}-m^{(1)}}\bold{V}^{(1)} \in \mathbb{R}^{B_r \times d} \\ m^{(2)} &= \max(m^{(1)},\text{rowmax}(\bold{S}^{(2)})) = m \\ \ell^{(2)} &= e^{m^{(1)}-m^{(2)}}\ell^{(1)} + \text{rowsum}(e^{\bold{S}^{(2)} - m^{(2)}}) \\ & = \text{rowsum}(e^{\bold{S}^{(1)} - m}) + \text{rowsum}(e^{\bold{S}^{(2)}-m}) = \ell \\ \tilde{\bold{P}}^{(2)} &= \text{diag}(\ell^{(2)})^{-1}e^{\bold{S}^{(2)}-m^{(2)}} \\ \tilde{\bold{O}}^{(2)} &= \text{diag}(e^{m^{(1)}-m^{(2)}})\tilde{\bold{O}}^{(1)} + e^{\bold{S}^{(2)}-m^{(2)}}\bold{V}^{(2)} = e^{\bold{S}^{(1)}-m}\bold{V}^{(1)} + e^{\bold{S}^{(2)}-m}\bold{V}^{(2)} \\ \bold{O}^{(2)} &= \text{diag}(\ell^{(2)})^{-1}\tilde{\bold{O}}^{(2)} = \bold{O} \end{aligned}
전체 Forward 알고리즘은 아래 참조. 추가로 병렬화를 위해 FlashAttention1과 달리 바깥 반복문에서 Q\bold{Q}를 반복하고, 내부 반복문에서 K,V\bold{K}, \bold{V}를 반복한다는 차이가 있다.
Algorithm - FlashAttention-2 forward pass
Require: HBM에서 행렬 Q,K,V∈RN×d\bold{Q}, \bold{K}, \bold{V} \in \mathbb{R}^{N\times d}, 블록 크기 Bc,BrB_c, B_r
1.
Q\bold{Q}를 각각 Br×dB_r \times d 크기의 Tr=⌈NBr⌉T_r = \lceil{N \over B_r}\rceil개 블록 Q1,...,QT\bold{Q}_1, ..., \bold{Q}_T으로 분할하고 K,V\bold{K}, \bold{V}를 각각 Bc×dB_c \times d 크기의 Tc=⌈NBc⌉T_c = \lceil{N \over B_c}\rceil개 블록 K1,...,KTc\bold{K}_1, ..., \bold{K}_{T_c}와 V1,...,VTc\bold{V}_1, ..., \bold{V}_{T_c}으로 분할
2.
O∈RN×d\bold{O} \in \mathbb{R}^{N \times d}를 각각 Br×dB_r \times d 크기의 TrT_r 개 블록 Oi,...,OTr\bold{O}_i, ... , \bold{O}_{T_r}으로 분할, log-sum-exp LL을 각각 크기 BrB_r의 TrT_r개 블록 Li,...,LTrL_i,...,L_{T_r}로 분할
3.
for 1≤i≤Tr1 \le i \le T_r do
a.
Qi\bold{Q}_i를 HBM에서 on-chip SRAM으로 로드
b.
on chip에서 Oi(0)=(0)Br×d∈RBr×d,ℓi(0)=(0)Br∈RBr,mi(0)=(−∞)Br∈RBr\bold{O}_i^{(0)} = (0)_{B_r \times d} \in \mathbb{R}^{B_r \times d}, \ell_i^{(0)} = (0)_{B_r} \in \mathbb{R}^{B_r}, m_i^{(0)} = (-\infty)_{B_r} \in \mathbb{R}^{B_r} 초기화
c.
for 1≤j≤Tc1 \le j \le T_c do
i.
Ki,Vj\bold{K}_i, \bold{V}_j를 HBM에서 on-chip SRAM으로 로드
ii.
on chip에서 Si(j)=QiKj⊤∈RBr×Bc\bold{S}_i^{(j)} = \bold{Q}_i\bold{K}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산
iii.
on chip에서 다음을 계산
•
mi(j)=max⁡(mi(j−1),rowmax(Si(j)))∈RBrm_i^{(j)} = \max(m_i^{(j-1)}, \text{rowmax}(\bold{S}_i^{(j)})) \in \mathbb{R}^{B_r}
•
P~i(j)=exp⁡(Si(j)−mi(j))∈RBr×Bc\tilde{\bold{P}}_i^{(j)} = \exp(\bold{S}_i^{(j)} - m_i^{(j)}) \in \mathbb{R}^{B_r \times B_c} (point-wise)
•
ℓi(j)=emij−1−mi(j)ℓi(j−1)+rowsum(P~i(j))∈RBr\ell_i^{(j)} = e^{m_i^{j-1}-m_i^{(j)}}\ell_i^{(j-1)} + \text{rowsum}(\tilde{\bold{P}}_i^{(j)}) \in \mathbb{R}^{B_r}
iv.
on chip에서 Oi(j)=diag(emi(j−1)−mi(j))Oi(j−1)+P~i(j)Vj\bold{O}_i^{(j)} = \text{diag}(e^{m_i^{(j-1)}-m_i^{(j)}})\bold{O}_i^{(j-1)} + \tilde{\bold{P}}_i^{(j)}\bold{V}_j 계산
d.
end for
e.
on chip에서 Oi=diag(ℓi(Tc))−1Oi(Tc)\bold{O}_i = \text{diag}(\ell_i^{(T_c)})^{-1}\bold{O}_i^{(T_c)} 계산
f.
on chip에서 Li=mi(Tc)+log⁡(ℓi(Tc))L_i = m_i^{(T_c)} + \log (\ell_i^{(T_c)}) 계산
g.
Oi\bold{O}_i를 O\bold{O}를 ii-번째 블록으로 HBM에 쓰기
h.
LiL_i를 LL를 ii-번째 블록으로 HBM에 쓰기
4.
end for
5.
출력 O\bold{O}와 log-sum-exp LL 반환

Backward Pass

FlashAttention 2의 Backward pass는 1과 거의 유사하지만, softmax에서 log-sum-exp LL을 사용한다는 점에만 차이가 있다. 전체 알고리즘은 아래 참조.
Algorithm 2. FlashAttention-2 Backward pass
Require: HBM에서 행렬 Q,K,V,O,dO∈RN×d\bold{Q}, \bold{K}, \bold{V}, \bold{O}, \bold{dO} \in \mathbb{R}^{N\times d}, HBM에서 벡터 L∈RNL \in \mathbb{R}^N, 블록 크기 Bc,BrB_c, B_r
1.
Q\bold{Q}를 각각 Br×dB_r \times d 크기의 Tr=⌈NBr⌉T_r = \lceil{N \over B_r}\rceil개 블록 Q1,...,QT\bold{Q}_1, ..., \bold{Q}_T으로 분할하고 K,V\bold{K}, \bold{V}를 각각 Bc×dB_c \times d 크기의 Tc=⌈NBc⌉T_c = \lceil{N \over B_c}\rceil개 블록 K1,...,KTc\bold{K}_1, ..., \bold{K}_{T_c}와 V1,...,VTc\bold{V}_1, ..., \bold{V}_{T_c}으로 분할
2.
O\bold{O}를 각각 Br×dB_r \times d 크기의 TrT_r 개 블록 Oi,...,OTr\bold{O}_i, ... , \bold{O}_{T_r}으로 분할, dO\bold{dO}를 각각 Br×dB_r \times d 크기의 TrT_r개 블록 dOi,...,dOTr\bold{dO}_i,...,\bold{dO}_{T_r}로 분할, LL을 각각 BrB_r 크기의 TrT_r개 블록 Li,...,LTrL_i,..., L_{T_r}로 분할
3.
HBM에서 dQ=(0)N×d\bold{dQ} = (0)_{N \times d}를 초기화하고 각각 Br×dB_r \times d 크기의 TrT_r개 블록 dQ1,...,dQTr\bold{dQ}_1,...,\bold{dQ}_{T_r}로 분할. dK,dV∈RN×d\bold{dK}, \bold{dV} \in \mathbb{R}^{N \times d}를 각각 Bc×dB_c \times d 크기의 TcT_c개 블록 dK1,...,dKTc\bold{dK}_1, ..., \bold{dK}_{T_c}와 dV1,...,dVTc\bold{dV}_1,...,\bold{dV}_{T_c}로 분할.
4.
D=rowsum(dO∘O)∈RdD = \text{rowsum}(\bold{dO} \circ \bold{O}) \in \mathbb{R}^d를 계산하고(pointwise 곱), DD를 HBM에 쓰고 각각 BrB_r 크기의 TrT_r개 블록 D1,..,DTrD_1, .., D_{T_r}로 분할
5.
for 1≤j≤Tc1 \le j \le T_c do
a.
Kj,Vj\bold{K}_j, \bold{V}_j를 HBM에서 on-chip SRAM으로 로드
b.
SRAM에서 dKj=(0)Bc×d,dVj=(0)Bc×d\bold{dK}_j = (0)_{B_c \times d}, \bold{dV}_j = (0)_{B_c \times d} 초기화
c.
for 1≤i≤Tr1 \le i \le T_r do
i.
Qi,Oi,dOi,dQi,Li,Di\bold{Q}_i, \bold{O}_i, \bold{dO}_i, \bold{dQ}_i, L_i, D_i를 HBM에서 on-chip SRAM으로 로드
ii.
on chip에서 Si(j)=QiKj⊤∈RBr×Bc\bold{S}_i^{(j)} = \bold{Q}_i\bold{K}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산
iii.
on chip에서 Pi(j)=exp⁡(Sij−Li)∈RBr×Bc\bold{P}_i^{(j)} = \exp(\bold{S}_{ij} - L_i) \in \mathbb{R}^{B_r \times B_c} 계산
iv.
on chip에서 dVj←dVj+(Pi(j))⊤dOi∈RBc×d\bold{dV}_j \leftarrow \bold{dV}_j + (\bold{P}_i^{(j)})^\top\bold{dO}_i \in \mathbb{R}^{B_c \times d} 계산
v.
on chip에서 dPi(j)=dOiVj⊤∈RBr×Bc\bold{dP}_i^{(j)} = \bold{dO}_i\bold{V}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산
vi.
on chip에서 dSi(j)=Pi(j)∘(dPi(j)−Di)∈RBr×Bc\bold{dS}_i^{(j)} = \bold{P}_i^{(j)} \circ (\bold{dP}_i^{(j)} - D_i) \in \mathbb{R}^{B_r \times B_c} 계산
vii.
dQi\bold{dQ}_i를 HBM에서 SRAM으로 로드하고 on chip에서 dQi←dQi+dSi(j)Kj∈RBr×d\bold{dQ}_i \leftarrow \bold{dQ}_i + \bold{dS}_i^{(j)}\bold{K}_j \in \mathbb{R}^{B_r \times d} 업데이트하고 HBM으로 다시 쓰기
viii.
on chip에서 dKj←dKj+dSi(j)⊤Qi∈RBc×d\bold{dK}_j \leftarrow \bold{dK}_j + \bold{dS}_i^{(j)\top}\bold{Q}_i \in \mathbb{R}^{B_c \times d} 계산
d.
end for
e.
dKj,dVj\bold{dK}_j, \bold{dV}_j를 HBM으로 쓰기
6.
end for
7.
dQ,dK,dV\bold{dQ}, \bold{dK}, \bold{dV} 반환

Parallelsim

Flash Attention 1은 batch 크기와 head 수에 따라 병렬화 하였지만, Flash Attention 2에서는 추가로 시퀀스 길이에 대해 병렬화를 추가한다. 이것은 GPU 점유율을 높이는데 도움이 된다.

Work Partitioning Between Warps

Flash Attention 1에서는 K\bold{K}와 V\bold{V}를 4개 warps 분할하는 반면 Q\bold{Q}는 모든 warps에 의해 접근 가능도록 유지한다. 이 경우 각 warp는 곱하여 QK⊤\bold{QK}^\top의 조각을 얻은 다음 V\bold{V}의 조각과 곱하고 결과를 합산하기 위해 통신해야 하는데, 이것을 ‘split-K’ 체제라고 한다. 그러나 이것은 모든 warps가 중간 결과를 shared 메모리에 기록하고, 동기화한 다음, 중간 결과를 합산해하기 때문에 비효율적이다. 이 shared 메모리 읽기/쓰기로 인해 forward pass를 느리게 한다.
Flash Attention 2에서 대신 Q\bold{Q}를 4개 warps으로 분할하면서 K\bold{K}와 V\bold{V}를 모든 warps에서 접근가능하게 한다. 각 wrap가 행렬 곱을 수행하여 QK⊤\bold{QK}^\top의 조각을 얻은 후, 공유된 V\bold{V}의 조각과 곱하면 해당 출력 조각을 얻을 수 있고, warps 사이의 통신이 필요하지 않다. shared 메모리에서의 읽기/쓰기가 축소되므로 속도 개선을 얻는다.
Backward pass에서도 ‘slip-K’ 체제를 피하기 위해 warp을 분할하지만 복잡한 의존성 관계로 완전히 제거는 못했다고 함.

Sample Code

Flash Attention의 flash_attn_interface.py에 다양한 attention 구현이 존재하지만 —가변 길이 또는 Packed 버전 등— 가장 기본적인 forward, backward에 대해서만 정리한다. Code는 Flash Attention 2를 기준으로 정리. 전체 소스는 아래 git 참조
flash-attention
Dao-AILab

Binding

외부 라이브러리가 python 상에서 Attention을 사용할 때는 flash_attn_interface.py 파일을 이용하지만, Flash Attention의 python은 아래와 같이 flash_api.cpp 파일에 연결되어 있다. 해당 파일은 flash_attn_2_cuda라는 이름으로 사용됨.
ext_modules.append( CUDAExtension( name="flash_attn_2_cuda", sources=[ "csrc/flash_attn/flash_api.cpp", "csrc/flash_attn/src/flash_fwd_hdim32_fp16_sm80.cu", "csrc/flash_attn/src/flash_fwd_hdim32_bf16_sm80.cu", ... ], ...
Python
복사
flash_api.cpp에서는 다시 아래와 같이 이름을 binding한다. 따라서 c++ 상에서 mha_fwd, mha_bwd라는 이름으로 구현된 함수를 python 상에서 fwd, bwd와 같은 이름으로 사용할 수 있다.
PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) { m.doc() = "FlashAttention"; m.def("fwd", &mha_fwd, "Forward pass"); m.def("varlen_fwd", &mha_varlen_fwd, "Forward pass (variable length)"); m.def("bwd", &mha_bwd, "Backward pass"); m.def("varlen_bwd", &mha_varlen_bwd, "Backward pass (variable length)"); m.def("fwd_kvcache", &mha_fwd_kvcache, "Forward pass, with KV-cache"); }
C++
복사
주의) CUDA에 구현된 forward와 backward 코드가 길고 복잡하므로, 데이터 Load와 설정, Write나 병렬화 관련 부분은 생략하고 알고리즘의 계산 단계에 해당하는 부분만 정리한다. 전체 코드가 CUDA에 맞춰 병렬화 되어 있기 때문에 일반적인 C++이나 python 코드처럼 직관적으로 이해하기는 쉽지 않다. 전체적인 흐름만 볼 것.

Forward

python 상에 구현된 _flash_attn_forward() 함수는 다음 단계를 거쳐 CUDA의 compute_attn_1rowblock()를 호출하고 Attention을 수행한다.
1.
python _flash_attn_forward() 에서 C++ mha_fwd() 호출
2.
mha_fwd()에서 각종 파라미터 설정 후에 run_mha_fwd() 호출
3.
run_mha_fwd()에서 run_mha_fwd_() 호출
•
만일 SplitKV 버전인 경우 run_mha_fwd_splitkv_dispatch() 호출
4.
run_mha_fwd_() 는 템플릿으로 run_mha_fwd_hdim64() ~ run_mha_fwd_hdim256() 호출하고 그 내부에서 run_flash_fwd() 호출
•
SplitKV 버전인 경우 run_mha_fwd_splitkv_dispatch() 에서 run_flash_splitkv_fwd() 호출
5.
run_flash_fwd() 는 flash_fwd_kernel 매크로 실행.
•
SplitKV 버전인 경우 run_flash_splitkv_fwd() 에서 flash_fwd_splitkv_kernel 매크로 실행
6.
flash_fwd_kernel 매크로에서 flash::compute_attn() 실행
•
SplitKV 버전인 경우 flash_fwd_splitkv_kernel 매크로에서 flash::compute_attn_splitkv() 실행
7.
flash::compute_attn() 에서 flash::compute_attn_1rowblock()을 실행해서 attention 수행
•
SplitKV 버전인 경우 flash::compute_attn_splitkv() 에서 flash::compute_attn_1rowblock_splitkv()을 실행해서 attention 수행
우선 forward 단계에 사용할 Q,K,V,O,L\bold{Q}, \bold{K}, \bold{V}, \bold{O}, L을 다음처럼 load한다. 알고리즘 상에는 반복문 전에 O,L\bold{O}, L를 load 하는 것으로 설명되지만, 실제 코드에서는 반복문 후에 load 함.
Tensor mQ = make_tensor(make_gmem_ptr(reinterpret_cast<Element*>(params.q_ptr) + binfo.q_offset(params.q_batch_stride, params.q_row_stride, bidb)), make_shape(binfo.actual_seqlen_q, params.h, params.d), make_stride(params.q_row_stride, params.q_head_stride, _1{})); Tensor gQ = local_tile(mQ(_, bidh, _), Shape<Int<kBlockM>, Int<kHeadDim>>{}, make_coord(m_block, 0)); // (kBlockM, kHeadDim) Tensor mK = make_tensor(make_gmem_ptr(reinterpret_cast<Element*>(params.k_ptr) + binfo.k_offset(params.k_batch_stride, params.k_row_stride, bidb)), make_shape(binfo.actual_seqlen_k, params.h_k, params.d), make_stride(params.k_row_stride, params.k_head_stride, _1{})); Tensor gK = local_tile(mK(_, bidh / params.h_h_k_ratio, _), Shape<Int<kBlockN>, Int<kHeadDim>>{}, make_coord(_, 0)); // (kBlockN, kHeadDim, nblocksN) Tensor mV = make_tensor(make_gmem_ptr(reinterpret_cast<Element*>(params.v_ptr) + binfo.k_offset(params.v_batch_stride, params.v_row_stride, bidb)), make_shape(binfo.actual_seqlen_k, params.h_k, params.d), make_stride(params.v_row_stride, params.v_head_stride, _1{})); Tensor gV = local_tile(mV(_, bidh / params.h_h_k_ratio, _), Shape<Int<kBlockN>, Int<kHeadDim>>{}, make_coord(_, 0)); // (kBlockN, kHeadDim, nblocksN) ... Tensor mO = make_tensor(make_gmem_ptr(reinterpret_cast<Element*>(params.o_ptr) + binfo.q_offset(params.o_batch_stride, params.o_row_stride, bidb)), make_shape(binfo.actual_seqlen_q, params.h, params.d), make_stride(params.o_row_stride, params.o_head_stride, _1{})); Tensor gO = local_tile(mO(_, bidh, _), Shape<Int<kBlockM>, Int<kHeadDim>>{}, make_coord(m_block, 0)); // (kBlockM, kHeadDim) Tensor mLSE = make_tensor(make_gmem_ptr(reinterpret_cast<ElementAccum*>(params.softmax_lse_ptr)), make_shape(params.b, params.h, params.seqlen_q), make_stride(params.h * params.seqlen_q, params.seqlen_q, _1{})); Tensor gLSE = local_tile(mLSE(bidb, bidh, _), Shape<Int<kBlockM>>{}, make_coord(m_block));
C++
복사
(내부 반복문에서)
1.
on chip에서 Si(j)=QiKj⊤∈RBr×Bc\bold{S}_i^{(j)} = \bold{Q}_i\bold{K}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산은 gemm()에서 한다.
flash::gemm</*A_in_regs=*/Kernel_traits::Is_Q_in_regs>( acc_s, tSrQ, tSrK, tSsQ, tSsK, tiled_mma, smem_tiled_copy_Q, smem_tiled_copy_K, smem_thr_copy_Q, smem_thr_copy_K );
C++
복사
template<bool A_in_regs=false, bool B_in_regs=false, typename Tensor0, typename Tensor1, typename Tensor2, typename Tensor3, typename Tensor4, typename TiledMma, typename TiledCopyA, typename TiledCopyB, typename ThrCopyA, typename ThrCopyB> __forceinline__ __device__ void gemm(Tensor0 &acc, Tensor1 &tCrA, Tensor2 &tCrB, Tensor3 const& tCsA, Tensor4 const& tCsB, TiledMma tiled_mma, TiledCopyA smem_tiled_copy_A, TiledCopyB smem_tiled_copy_B, ThrCopyA smem_thr_copy_A, ThrCopyB smem_thr_copy_B) { CUTE_STATIC_ASSERT_V(size<1>(tCrA) == size<1>(acc)); // MMA_M CUTE_STATIC_ASSERT_V(size<1>(tCrB) == size<2>(acc)); // MMA_N CUTE_STATIC_ASSERT_V(size<2>(tCrA) == size<2>(tCrB)); // MMA_K Tensor tCrA_copy_view = smem_thr_copy_A.retile_D(tCrA); CUTE_STATIC_ASSERT_V(size<1>(tCsA) == size<1>(tCrA_copy_view)); // M Tensor tCrB_copy_view = smem_thr_copy_B.retile_D(tCrB); CUTE_STATIC_ASSERT_V(size<1>(tCsB) == size<1>(tCrB_copy_view)); // N if (!A_in_regs) { cute::copy(smem_tiled_copy_A, tCsA(_, _, _0{}), tCrA_copy_view(_, _, _0{})); } if (!B_in_regs) { cute::copy(smem_tiled_copy_B, tCsB(_, _, _0{}), tCrB_copy_view(_, _, _0{})); } #pragma unroll for (int i = 0; i < size<2>(tCrA); ++i) { if (i < size<2>(tCrA) - 1) { if (!A_in_regs) { cute::copy(smem_tiled_copy_A, tCsA(_, _, i + 1), tCrA_copy_view(_, _, i + 1)); } if (!B_in_regs) { cute::copy(smem_tiled_copy_B, tCsB(_, _, i + 1), tCrB_copy_view(_, _, i + 1)); } } cute::gemm(tiled_mma, tCrA(_, _, i), tCrB(_, _, i), acc); } }
C++
복사
2.
on chip에서 다음을 계산하는 코드는 softmax_rescale_o()에서 한다.
•
mi(j)=max⁡(mi(j−1),rowmax(Si(j)))∈RBrm_i^{(j)} = \max(m_i^{(j-1)}, \text{rowmax}(\bold{S}_i^{(j)})) \in \mathbb{R}^{B_r}
•
P~i(j)=exp⁡(Si(j)−mi(j))∈RBr×Bc\tilde{\bold{P}}_i^{(j)} = \exp(\bold{S}_i^{(j)} - m_i^{(j)}) \in \mathbb{R}^{B_r \times B_c} (point-wise)
•
ℓi(j)=emij−1−mi(j)ℓi(j−1)+rowsum(P~i(j))∈RBr\ell_i^{(j)} = e^{m_i^{j-1}-m_i^{(j)}}\ell_i^{(j-1)} + \text{rowsum}(\tilde{\bold{P}}_i^{(j)}) \in \mathbb{R}^{B_r}
softmax.template softmax_rescale_o</*Is_first=*/false, /*Check_inf=*/Is_local>(acc_s, acc_o, params.scale_softmax_log2);
C++
복사
template<bool Is_first, bool Check_inf=false, typename Tensor0, typename Tensor1> __forceinline__ __device__ void softmax_rescale_o(Tensor0 &acc_s, Tensor1 &acc_o, float softmax_scale_log2) { // Reshape acc_s from (MMA=4, MMA_M, MMA_N) to (nrow=(2, MMA_M), ncol=(2, MMA_N)) Tensor scores = make_tensor(acc_s.data(), flash::convert_layout_acc_rowcol(acc_s.layout())); static_assert(decltype(size<0>(scores))::value == kNRows); if (Is_first) { flash::template reduce_max</*zero_init=*/true>(scores, row_max); flash::scale_apply_exp2(scores, row_max, softmax_scale_log2); flash::reduce_sum</*zero_init=*/true>(scores, row_sum); } else { Tensor scores_max_prev = make_fragment_like(row_max); cute::copy(row_max, scores_max_prev); flash::template reduce_max</*zero_init=*/false>(scores, row_max); // Reshape acc_o from (MMA=4, MMA_M, MMA_K) to (nrow=(2, MMA_M), ncol=(2, MMA_K)) Tensor acc_o_rowcol = make_tensor(acc_o.data(), flash::convert_layout_acc_rowcol(acc_o.layout())); static_assert(decltype(size<0>(acc_o_rowcol))::value == kNRows); #pragma unroll for (int mi = 0; mi < size(row_max); ++mi) { float scores_max_cur = !Check_inf ? row_max(mi) : (row_max(mi) == -INFINITY ? 0.0f : row_max(mi)); float scores_scale = exp2f((scores_max_prev(mi) - scores_max_cur) * softmax_scale_log2); row_sum(mi) *= scores_scale; #pragma unroll for (int ni = 0; ni < size<1>(acc_o_rowcol); ++ni) { acc_o_rowcol(mi, ni) *= scores_scale; } } flash::scale_apply_exp2(scores, row_max, softmax_scale_log2); // We don't do the reduce across threads here since we don't need to use the row_sum. // We do that reduce at the end when we need to normalize the softmax. flash::reduce_sum</*zero_init=*/false>(scores, row_sum); } };
C++
복사
3.
on chip에서 Oi(j)=diag(emi(j−1)−mi(j))Oi(j−1)+P~i(j)Vj\bold{O}_i^{(j)} = \text{diag}(e^{m_i^{(j-1)}-m_i^{(j)}})\bold{O}_i^{(j-1)} + \tilde{\bold{P}}_i^{(j)}\bold{V}_j 계산은 gemm_rs()에서 한다.
Tensor tOrP = make_tensor(rP.data(), flash::convert_layout_acc_Aregs<Kernel_traits::TiledMma>(rP.layout())); flash::gemm_rs(acc_o, tOrP, tOrVt, tOsVt, tiled_mma, smem_tiled_copy_V, smem_thr_copy_V);
C++
복사
template<typename Tensor0, typename Tensor1, typename Tensor2, typename Tensor3, typename TiledMma, typename TiledCopy, typename ThrCopy> __forceinline__ __device__ void gemm_rs(Tensor0 &acc, Tensor1 &tCrA, Tensor2 &tCrB, Tensor3 const& tCsB, TiledMma tiled_mma, TiledCopy smem_tiled_copy_B, ThrCopy smem_thr_copy_B) { CUTE_STATIC_ASSERT_V(size<1>(tCrA) == size<1>(acc)); // MMA_M CUTE_STATIC_ASSERT_V(size<1>(tCrB) == size<2>(acc)); // MMA_N CUTE_STATIC_ASSERT_V(size<2>(tCrA) == size<2>(tCrB)); // MMA_K Tensor tCrB_copy_view = smem_thr_copy_B.retile_D(tCrB); CUTE_STATIC_ASSERT_V(size<1>(tCsB) == size<1>(tCrB_copy_view)); // N cute::copy(smem_tiled_copy_B, tCsB(_, _, _0{}), tCrB_copy_view(_, _, _0{})); #pragma unroll for (int i = 0; i < size<2>(tCrA); ++i) { if (i < size<2>(tCrA) - 1) { cute::copy(smem_tiled_copy_B, tCsB(_, _, i + 1), tCrB_copy_view(_, _, i + 1)); } cute::gemm(tiled_mma, tCrA(_, _, i), tCrB(_, _, i), acc); } }
C++
복사
(내부 반복문 종료 후에)
1.
on chip에서 Oi=diag(ℓi(Tc))−1Oi(Tc)\bold{O}_i = \text{diag}(\ell_i^{(T_c)})^{-1}\bold{O}_i^{(T_c)} 계산은 아래 normalize_softmax_lse()에서 한다.
Tensor lse = softmax.template normalize_softmax_lse<Is_dropout>(acc_o, params.scale_softmax, params.rp_dropout);
C++
복사
template<bool Is_dropout=false, bool Split=false, typename Tensor0> __forceinline__ __device__ TensorT normalize_softmax_lse(Tensor0 &acc_o, float softmax_scale, float rp_dropout=1.0) { SumOp<float> sum_op; quad_allreduce_(row_sum, row_sum, sum_op); TensorT lse = make_fragment_like(row_sum); Tensor acc_o_rowcol = make_tensor(acc_o.data(), flash::convert_layout_acc_rowcol(acc_o.layout())); static_assert(decltype(size<0>(acc_o_rowcol))::value == kNRows); #pragma unroll for (int mi = 0; mi < size<0>(acc_o_rowcol); ++mi) { float sum = row_sum(mi); float inv_sum = (sum == 0.f || sum != sum) ? 1.f : 1.f / sum; lse(mi) = (sum == 0.f || sum != sum) ? (Split ? -INFINITY : INFINITY) : row_max(mi) * softmax_scale + __logf(sum); float scale = !Is_dropout ? inv_sum : inv_sum * rp_dropout; #pragma unroll for (int ni = 0; ni < size<1>(acc_o_rowcol); ++ni) { acc_o_rowcol(mi, ni) *= scale; } } return lse; };
C++
복사
2.
on chip에서 Li=mi(Tc)+log⁡(ℓi(Tc))L_i = m_i^{(T_c)} + \log (\ell_i^{(T_c)}) 계산은 아래 코드에서 한다.
Tensor caccO = make_identity_tensor(Shape<Int<kBlockM>, Int<kHeadDim>>{}); // (BLK_M,BLK_K) -> (blk_m,blk_k) Tensor taccOcO = thr_mma.partition_C(caccO); // (MMA,MMA_M,MMA_K) static_assert(decltype(size<0>(taccOcO))::value == 4); // Convert to ((2, 2), MMA_M, MMA_K) then take only the row indices. Tensor taccOcO_row = logical_divide(taccOcO, Shape<_2>{})(make_coord(0, _), _, 0); CUTE_STATIC_ASSERT_V(size(lse) == size(taccOcO_row)); // MMA_M if (get<1>(taccOcO_row(0)) == 0) { #pragma unroll for (int mi = 0; mi < size(lse); ++mi) { const int row = get<0>(taccOcO_row(mi)); if (row < binfo.actual_seqlen_q - m_block * kBlockM) { gLSE(row) = lse(mi); } } }
C++
복사

Backward

python 상에 구현된 _flash_attn_backward() 함수는 다음 단계를 거쳐 CUDA의 compute_dq_dk_dv_1colblock()를 호출하여 Attention Recomputateion과 Gradient 계산을 수행한다.
1.
python _flash_attn_backward() 에서 C++ mha_bwd() 호출
2.
mha_bwd()에서 각종 파라미터 설정 후에 run_mha_bwd() 호출
3.
run_mha_bwd()에서 run_mha_bwd_() 호출
4.
run_mha_bwd_() 는 템플릿으로 run_mha_bwd_hdim32() ~ run_mha_bwd_hdim256() 호출하고 그 내부에서 run_flash_bwd() 호출
5.
run_flash_bwd() 는 run_flash_bwd_seqk_parallel() 실행.
6.
run_flash_bwd_seqk_parallel()는 내부에서 flash_bwd_dq_dk_dv_loop_seqk_parallel_kernel 매크로 실행
7.
flash_bwd_dq_dk_dv_loop_seqk_parallel_kernel 매크로에서 flash::compute_dq_dk_dv_seqk_parallel() 실행
8.
flash::compute_dq_dk_dv_seqk_parallel() 에서 flash::compute_dq_dk_dv_1colblock()을 실행해서 attention 수행
우선 backward 단계에서 사용할 Q,K,V,O,dO,dQ,L\bold{Q}, \bold{K}, \bold{V}, \bold{O}, \bold{dO}, \bold{dQ}, L를 다음처럼 load한다. dK,dV\bold{dK}, \bold{dV}는 반복문에서 사용됨.
Tensor gQ = make_tensor(make_gmem_ptr(reinterpret_cast<Element *>(params.q_ptr) + row_offset_q), Shape<Int<kBlockM>, Int<kHeadDim>>{}, make_stride(params.q_row_stride, _1{})); Tensor gK = make_tensor(make_gmem_ptr(reinterpret_cast<Element *>(params.k_ptr) + row_offset_k), Shape<Int<kBlockN>, Int<kHeadDim>>{}, make_stride(params.k_row_stride, _1{})); Tensor gV = make_tensor(make_gmem_ptr(reinterpret_cast<Element *>(params.v_ptr) + row_offset_v), Shape<Int<kBlockN>, Int<kHeadDim>>{}, make_stride(params.v_row_stride, _1{})); Tensor gdO = make_tensor(make_gmem_ptr(reinterpret_cast<Element *>(params.do_ptr) + row_offset_do), Shape<Int<kBlockM>, Int<kHeadDim>>{}, make_stride(params.do_row_stride, _1{})); Tensor gO = make_tensor(make_gmem_ptr(reinterpret_cast<Element *>(params.o_ptr) + row_offset_o), Shape<Int<kBlockM>, Int<kHeadDim>>{}, make_stride(params.o_row_stride, _1{})); Tensor gdQ = make_tensor(make_gmem_ptr(reinterpret_cast<Element *>(params.dq_ptr) + row_offset_dq), Shape<Int<kBlockM>, Int<kHeadDim>>{}, make_stride(params.dq_row_stride, _1{})); Tensor gdQaccum = make_tensor(make_gmem_ptr(reinterpret_cast<ElementAccum *>(params.dq_accum_ptr) + row_offset_dq_accum), Shape<Int<kBlockM>, Int<kHeadDim>>{}, make_stride(params.h * params.d_rounded, _1{})); Tensor gLSE = make_tensor(make_gmem_ptr(reinterpret_cast<ElementAccum *>(params.softmax_lse_ptr) + row_offset_lse), Shape<Int<kBlockM>>{}, Stride<_1>{}); Tensor gdPsum = make_tensor(make_gmem_ptr(reinterpret_cast<ElementAccum *>(params.dsoftmax_sum) + row_offset_dpsum), Shape<Int<kBlockM>>{}, Stride<_1>{});
C++
복사
다음으로 반복문 내에서 사용할 D=rowsum(dO∘O)∈RdD = \text{rowsum}(\bold{dO} \circ \bold{O}) \in \mathbb{R}^d를 다음과 같이 한다. 여기서 gdPsum은 위에서 load한 tensor이다.
Tensor dP_sum = make_fragment_like(lse); #pragma unroll for (int mi = 0; mi < size(lse); ++mi) { dP_sum(mi) = gdPsum(get<0>(taccScS_row(mi))); }
C++
복사
(반복문에서)
1.
Si(j)=QiKj⊤∈RBr×Bc\bold{S}_i^{(j)} = \bold{Q}_i\bold{K}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산은 gemm()에서 한다. (gemm() 코드는 forward 참조)
flash::gemm(acc_s, tSrQ, tSrK, tSsQ, tSsK, tiled_mma_sdp, smem_tiled_copy_QdO, smem_tiled_copy_KV, smem_thr_copy_QdO, smem_thr_copy_KV);
C++
복사
2.
Pi(j)=exp⁡(Sij−Li)∈RBr×Bc\bold{P}_i^{(j)} = \exp(\bold{S}_{ij} - L_i) \in \mathbb{R}^{B_r \times B_c} 계산은 scale_apply_exp2()에서 한다. 여기서 lse는 forward 단계에서 계산한 값이다.
flash::scale_apply_exp2</*scale_max=*/false>(scores, lse, params.scale_softmax_log2); if constexpr (Is_dropout) { int warp_id = tidx / 32; int block_row_idx = m_block * (kBlockM / 16) + warp_id % AtomLayoutMS; // Need col to be multiples of 32, since we're doing dropout with block of 16 x 32 static_assert(MMA_N_SdP % 2 == 0); int block_col_idx = n_block * (kBlockN / 32) + (warp_id / AtomLayoutMS) * (MMA_N_SdP / 2); dropout.template apply_dropout</*encode_dropout_in_sign_bit=*/true>( acc_s, block_row_idx, block_col_idx, AtomLayoutMS ); }
C++
복사
template <bool Scale_max=true, typename Engine0, typename Layout0, typename Engine1, typename Layout1> __forceinline__ __device__ void scale_apply_exp2(Tensor<Engine0, Layout0> &tensor, Tensor<Engine1, Layout1> const &max, const float scale) { static_assert(Layout0::rank == 2, "Only support 2D Tensor"); static_assert(Layout1::rank == 1, "Only support 1D Tensor"); CUTE_STATIC_ASSERT_V(size<0>(max) == size<0>(tensor)); #pragma unroll for (int mi = 0; mi < size<0>(tensor); ++mi) { // If max is -inf, then all elements must have been -inf (possibly due to masking). // We don't want (-inf - (-inf)) since that would give NaN. // If we don't have float around M_LOG2E the multiplication is done in fp64. const float max_scaled = max(mi) == -INFINITY ? 0.f : max(mi) * (Scale_max ? scale : float(M_LOG2E)); #pragma unroll for (int ni = 0; ni < size<1>(tensor); ++ni) { // Instead of computing exp(x - max), we compute exp2(x * log_2(e) - // max * log_2(e)) This allows the compiler to use the ffma // instruction instead of fadd and fmul separately. // The following macro will disable the use of fma. // See: https://github.com/pytorch/pytorch/issues/121558 for more details // This macro is set in PyTorch and not FlashAttention #ifdef UNFUSE_FMA tensor(mi, ni) = exp2f(__fmul_rn(tensor(mi, ni), scale) - max_scaled); #else tensor(mi, ni) = exp2f(tensor(mi, ni) * scale - max_scaled); #endif } } }
C++
복사
3.
dVj←dVj+(Pi(j))⊤dOi∈RBc×d\bold{dV}_j \leftarrow \bold{dV}_j + (\bold{P}_i^{(j)})^\top\bold{dO}_i \in \mathbb{R}^{B_c \times d} 계산은 gemm()에서 한다.
flash::gemm</*A_in_regs=*/false, /*B_in_regs=*/Kernel_traits::Is_V_in_regs>( acc_dp, tdPrdO, tdPrV, tdPsdO, tdPsV, tiled_mma_sdp, smem_tiled_copy_QdO, smem_tiled_copy_KV, smem_thr_copy_QdO, smem_thr_copy_KV );
C++
복사
4.
dPi(j)=dOiVj⊤∈RBr×Bc\bold{dP}_i^{(j)} = \bold{dO}_i\bold{V}_j^\top \in \mathbb{R}^{B_r \times B_c} 계산은 gemm()에서 한다.
flash::gemm(acc_dv, tdVrPt, tdVrdO, tdVsPt, tdVsdOt, tiled_mma_dkv, smem_tiled_copy_PdSt, smem_tiled_copy_QdOt, smem_thr_copy_PdSt, smem_thr_copy_QdOt);
C++
복사
5.
dSi(j)=Pi(j)∘(dPi(j)−Di)∈RBr×Bc\bold{dS}_i^{(j)} = \bold{P}_i^{(j)} \circ (\bold{dP}_i^{(j)} - D_i) \in \mathbb{R}^{B_r \times B_c} 계산은 다음과 같이 한다.
// Reshape acc_dp from (MMA=4, MMA_N, MMA_N) to (col=(2, MMA_N), row=(2, MMA_N)) Tensor dS = make_tensor(acc_dp.data(), scores.layout()); auto pointwise_mult = [](float p, float dp, float d) { return p * (!Is_dropout || p >= 0 ? dp - d : d); }; #pragma unroll for (int mi = 0; mi < size<0>(dS); ++mi) { #pragma unroll for (int ni = 0; ni < size<1>(dS); ++ni) { dS(mi, ni) = pointwise_mult(scores(mi, ni), dS(mi, ni), dP_sum(mi)); } }
C++
복사
6.
dQi←dQi+dSi(j)Kj∈RBr×d\bold{dQ}_i \leftarrow \bold{dQ}_i + \bold{dS}_i^{(j)}\bold{K}_j \in \mathbb{R}^{B_r \times d} 계산은 gemm()에서 한다.
flash::gemm(acc_dq, tdQrdS, tdQrKt, tdQsdS, tdQsKt, tiled_mma_dq, smem_tiled_copy_dS, smem_tiled_copy_Kt, smem_thr_copy_dS, smem_thr_copy_Kt);
C++
복사
7.
dKj←dKj+dSi(j)⊤Qi∈RBc×d\bold{dK}_j \leftarrow \bold{dK}_j + \bold{dS}_i^{(j)\top}\bold{Q}_i \in \mathbb{R}^{B_c \times d} 계산은 gemm()에서 한다.
flash::gemm(acc_dk, tdKrdSt, tdKrQt, tdKsdSt, tdKsQt, tiled_mma_dkv, smem_tiled_copy_PdSt, smem_tiled_copy_QdOt, smem_thr_copy_PdSt, smem_thr_copy_QdOt);
C++
복사

참고

Made with