Search
Duplicate

AI/ Camera Projection Matrix

Camera Projection Matrix

Camera Projection Matrix는 3d 점을 카메라 이미지 평면에 투영하기 위한 변환을 나타내는 행렬로 일반적으로 다음과 같이 표현된다.
P=K[Rt]\bold{P} = \bold{K}\begin{bmatrix} \bold{R} \quad \bold{t}\end{bmatrix}
여기서 P\bold{P}는 3×43\times 4 projection matrix이고, K\bold{K}는 3×33\times 3 intrinsic matrix이고, R\bold{R}은 3×33\times 3 rotation matrix이고, t\bold{t}는 3×13\times 1 translation vector이다.
카메라가 이동하거나 회전하면 카메라 투영 행렬을 다시 계산해야 한다는 점에 유의하라.
3d 점 P=(x,y,z)P = (x, y, z) 2d 이미지 평면의 점 pp에 투영하기 위해 우선 homogeneous(동차) 좌표계로 확장하여 Ph=(x,y,z,1)P_h = (x, y, z, 1)로 나타낸 다음, 이를 camera projection matrix와 곱해서 다음과 같이 2d homogeneous 좌표 ph=(x,y,w)p_h = (x, y, w)를 얻는다.
ph=PPh=K[Rt]Php_h = \bold{P} P_h = \bold{K}\begin{bmatrix} \bold{R} \quad \bold{t}\end{bmatrix}P_h
그 다음 homogeneous 좌표 ph=(x,y,w)p_h = (x, y, w)를 아래와 같이 정규화하여 최종적으로 이미지 평면의 점 p=(x,y)p = (x, y)을 얻는다.
p=(xw,yw)p = \left({x \over w}, {y\over w}\right)
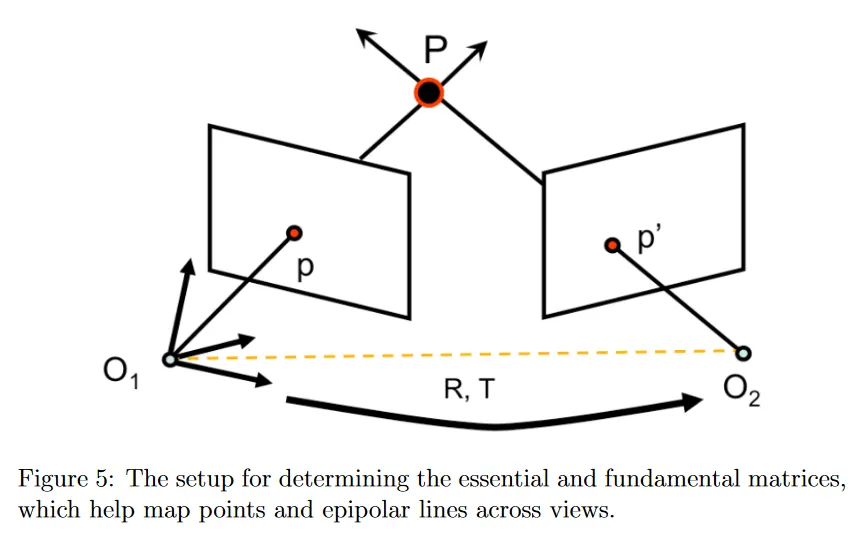
epipolar geometry framework에서 첫 번째 카메라를 기준계로 설정하고 두 번째 카메라가 첫 번째 카메라에 대해 RR의 회전과 TT의 평행이동된 것이라고 가정하면, 두 카메라의 Camera Projection Matrix M,M′M, M'를 다음과 같이 정의할 수 있다.
M=K[I0]M′=K′[R⊤−R⊤T]\begin{aligned} M &= K\begin{bmatrix} I & 0 \end{bmatrix} \\ M' &= K'\begin{bmatrix} R^\top & -R^\top T \end{bmatrix} \end{aligned}
첫 번째 카메라가 기준계이므로 원점에 위치하고 방향이 월드 좌표계와 일치한다. 첫 번째 카메라의 위치를 두 번째 카메라로 평행이동 시키는 TT는 baseline 벡터가 되며, 따라서 TT의 크기는 baseline의 길이가 된다. TT가 baseline 벡터이므로 TT는 3d점 PP와 두 카메라의 원점 O1,O2O_1, O_2를 포함하는 epipolar plane 위에 놓이게 된다.
카메라 투영 행렬의 개념은 위와 같지만, 실제로는 투영된 2d 점의 위치를 이용하여 3d 점의 위치를 거꾸로 계산하는데 관심이 있다. 이것은 Triangulation을 이용하여 계산할 수 있다. 다음 페이지 참조. AI/ Triangulation

참고

Made with